3 formas de calcular la presión de vapor

2024 Autor: Jason Gerald | [email protected]. Última modificación: 2024-02-01 14:12

¿Alguna vez ha dejado una botella de agua al sol durante unas horas y escuchó un leve "silbido" cuando la abrió? Esto se debe a un principio llamado presión de vapor. En química, la presión de vapor es la presión que ejercen las paredes de un recipiente cerrado cuando la sustancia química que contiene se evapora (se convierte en gas). Para encontrar la presión de vapor a una temperatura dada, use la ecuación de Clausius-Clapeyron: ln (P1 / P2) = (ΔH_vapor/ R) ((1 / T2) - (1 / T1)).

Paso

Método 1 de 3: Uso de la ecuación de Clausius-Clapeyron

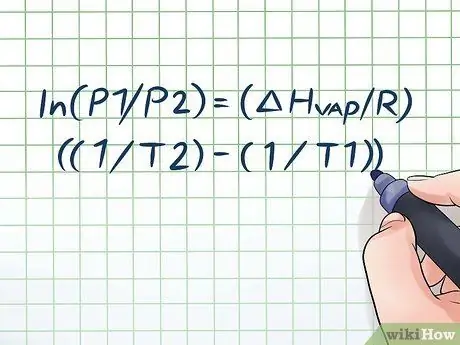
Paso 1. Escribe la ecuación de Clausius-Clapeyron

La fórmula utilizada para calcular la presión de vapor con el cambio en la presión de vapor a lo largo del tiempo se llama ecuación de Clausius-Clapeyron (llamada así por los físicos Rudolf Clausius y Benoît Paul mile Clapeyron). Esta es básicamente la fórmula que necesitará para resolver la mayoría de los tipos de problemas. Las preguntas sobre la presión de vapor se encuentran a menudo en las clases de física y química. La fórmula es así: ln (P1 / P2) = (ΔH_vapor/ R) ((1 / T2) - (1 / T1)). En esta fórmula, las variables representan:

H_vapor:

La entalpía de vaporización de un líquido. Esta entalpía generalmente se puede encontrar en la tabla al final del libro de texto de química.
R:

La constante de gas real / universal, o 8,314 J / (K × Mol).
Q1:

La temperatura a la que se conoce la presión de vapor (o temperatura inicial).
T2:

La temperatura a la que se desconoce / desea encontrar la presión de vapor (o la temperatura final).
P1 y P2:

Presión de vapor a las temperaturas T1 y T2, respectivamente.

Paso 2. Ingrese las variables que conoce

La ecuación de Clausius-Clapeyron parece complicada porque tiene muchas variables diferentes, pero en realidad no es tan difícil si tienes la información correcta. La mayoría de los problemas básicos de presión de vapor enumerarán dos valores de temperatura y un valor de presión o dos valores de presión y un valor de temperatura; una vez que se dé cuenta de eso, resolver esta ecuación es muy fácil.

Por ejemplo, digamos que se nos dice que tenemos un recipiente lleno de líquido a 295 K cuya presión de vapor es 1 atmósfera (atm). Nuestra pregunta es: ¿Cuál es la presión de vapor a 393 K? Tenemos dos valores de temperatura y un valor de presión, por lo que podemos encontrar los otros valores de presión usando la ecuación de Clausius-Clapeyron. Al conectar nuestras variables, obtenemos ln (1 / P2) = (ΔH_vapor/ R) ((1/393) - (1/295)).
Tenga en cuenta que, para la ecuación de Clausius-Clapeyron, siempre debe usar el valor de temperatura Kelvin. Puede utilizar cualquier valor de presión siempre que los valores de P1 y P2 sean los mismos.

Paso 3. Ingrese sus constantes

La ecuación de Clausius-Clapeyron tiene dos constantes: R y H_vapor. R siempre es igual a 8,314 J / (K × Mol). Sin embargo, H_vapor (entalpía de vaporización) depende de la sustancia cuya presión de vapor esté buscando. Como se señaló anteriormente, generalmente puede encontrar los valores de H_vapor para varias sustancias en la parte posterior de un libro de texto de química o física, o en línea (como, por ejemplo, aquí).

En nuestro ejemplo, supongamos que nuestro líquido es agua pura.

Si miramos en la tabla los valores de H_vapor, encontramos que H_vapor el agua pura es de aproximadamente 40,65 KJ / mol. Dado que nuestro valor de H está en julios y no en kilojulios, podemos convertirlo a 40.650 J / mol.
Conectando nuestras constantes, obtenemos ln (1 / P2) = (40,650 / 8,314) ((1/393) - (1/295)).

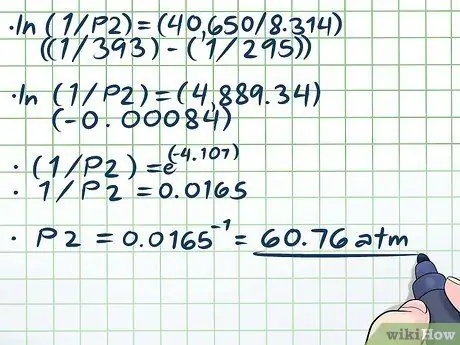
Paso 4. Resuelve la ecuación

Una vez que hayas incluido todas las variables en la ecuación excepto la que estás buscando, procede a resolver la ecuación de acuerdo con las reglas del álgebra ordinaria.

La única parte difícil de resolver nuestra ecuación (ln (1 / P2) = (40,650 / 8,314) ((1/393) - (1/295))) está resolviendo el logaritmo natural (ln). Para eliminar el logaritmo natural, simplemente use ambos lados de la ecuación como exponentes de la constante matemática e. En otras palabras, ln (x) = 2 → e^{en (x)} = e² → x = e².
Ahora, resolvamos nuestra ecuación:
ln (1 / P2) = (40,650 / 8,314) ((1/393) - (1/295))
ln (1 / P2) = (4889, 34) (- 0, 00084)
(1 / P2) = e^{(-4, 107)}
1 / P2 = 0,0165
P2 = 0.0165^-1 = 60, 76 atm.

Esto tiene sentido: en un recipiente cerrado, elevar la temperatura a casi 100 grados (a casi 20 grados por encima del punto de ebullición) producirá mucho vapor, aumentando la presión rápidamente.

Método 2 de 3: encontrar la presión de vapor con una solución disuelta

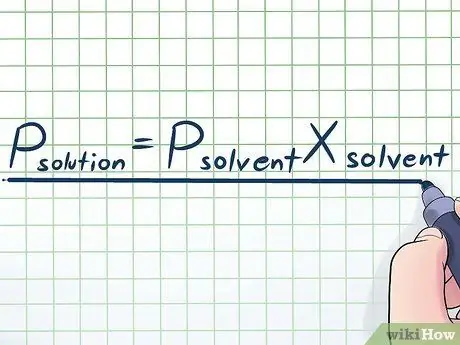
Paso 1. Escriba la ley de Raoult

En la vida real, rara vez trabajamos con un líquido puro; por lo general, trabajamos con un líquido que es una mezcla de varias sustancias diferentes. Algunas de las mezclas más comúnmente utilizadas se obtienen disolviendo una pequeña cantidad de un determinado químico llamado soluto en muchos químicos llamados solventes para hacer una solución. En estos casos, es útil conocer una ecuación llamada Ley de Raoult (que lleva el nombre del físico François-Marie Raoult), que se escribe así: PAG_{sustancia disoluta}= P_solventeX_solvente. En esta fórmula, las variables representan;

PAG_{sustancia disoluta}:

Presión de vapor de toda la solución (todos los elementos combinados)
PAG_solvente:

Presión de vapor de disolvente
X_solvente:

Fracción molar de disolvente
No se preocupe si no conoce términos como fracción molar; los explicaremos en los siguientes pasos.

Paso 2. Determine el solvente y el soluto en su solución

Antes de poder calcular la presión de vapor de un líquido mezclado, debe identificar las sustancias que está usando. Como recordatorio, se forma una solución cuando un soluto se disuelve en un solvente; el químico que se disuelve siempre se llama soluto, y el químico que lo disuelve siempre se llama solvente.

Trabajemos usando los ejemplos simples de esta sección para ilustrar los conceptos que discutimos. Para nuestro ejemplo, digamos que queremos encontrar la presión de vapor del jarabe de azúcar. Tradicionalmente, el jarabe de azúcar es azúcar soluble en agua (proporción 1: 1), por lo que podemos decir que el azúcar es nuestro soluto y el agua es nuestro solvente.
Tenga en cuenta que la fórmula química de la sacarosa (azúcar de mesa) es C₁₂H₂₂O₁₁. Esta fórmula química será muy importante.

Paso 3. Encuentra la temperatura de la solución

Como vimos en la sección de Clausius Clapeyron anterior, la temperatura de un líquido afectará su presión de vapor. Generalmente, cuanto mayor es la temperatura, mayor es la presión de vapor; a medida que aumenta la temperatura, más líquido se evapora y forma vapor, lo que aumenta la presión en el recipiente.

En nuestro ejemplo, digamos que la temperatura del jarabe de azúcar en este punto es 298 K (alrededor de 25 C).

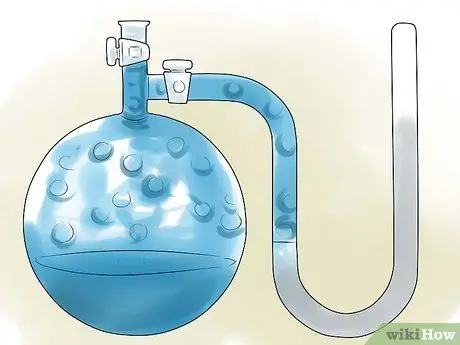
Paso 4. Encuentre la presión de vapor del solvente

Los materiales químicos de referencia suelen tener valores de presión de vapor para muchas sustancias y compuestos de uso común, pero estos valores de presión generalmente solo son válidos si la sustancia tiene una temperatura de 25 C / 298 K o su punto de ebullición. Si su solución tiene una de estas temperaturas, puede usar un valor de referencia, pero si no, deberá encontrar la presión de vapor a esa temperatura.

El Clausius-Clapeyron puede ayudar: use una presión de vapor de referencia y 298 K (25 C) para P1 y T1 respectivamente.
En nuestro ejemplo, nuestra mezcla tiene una temperatura de 25 C, por lo que podemos usar fácilmente nuestra tabla de referencia fácil. Sabemos que a 25 C, el agua tiene una presión de vapor de 23,8 mm HG

Paso 5. Encuentra la fracción molar de tu solvente

Lo último que debemos hacer antes de resolver esto es encontrar la fracción molar de nuestro solvente. Encontrar la fracción molar es fácil: simplemente convierta sus compuestos en moles, luego encuentre el porcentaje de cada compuesto en el número total de moles de la sustancia. En otras palabras, la fracción molar de cada compuesto es igual a (moles de compuesto) / (número total de moles en sustancia).

Supongamos que nuestra receta para usos de jarabe de azúcar 1 litro (L) de agua y 1 litro de sacarosa (azúcar).

En este caso, debemos encontrar el número de moles de cada compuesto. Para hacer esto, encontraremos la masa de cada compuesto, luego usaremos la masa molar de la sustancia para convertirla en moles.
Masa (1 L de agua): 1.000 gramos (g)
Masa (1 L de azúcar sin refinar): Aprox. 1056,8 g
Moles (agua): 1,000 gramos × 1 mol / 18.015 g = 55.51 mol
Moles (sacarosa): 1,056, 7 gramos × 1 mol / 342,2965 g = 3,08 moles (tenga en cuenta que puede encontrar la masa molar de sacarosa a partir de su fórmula química, C₁₂H₂₂O₁₁.)
Total de moles: 55,51 + 3,08 = 58,59 mol
Fracción molar de agua: 55, 51/58, 59 = 0, 947

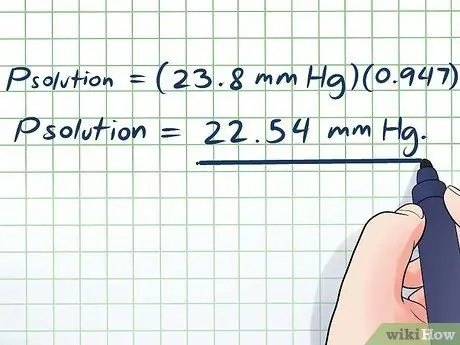
Paso 6. Termina

Finalmente, tenemos todo lo que necesitamos para resolver nuestra ecuación de la Ley de Raoult. Esta parte es muy fácil: simplemente ingrese sus valores para las variables en la ecuación simplificada de la Ley de Raoult al comienzo de esta sección (PAG_{sustancia disoluta} = P_solventeX_solvente).

Ingresando nuestros valores, obtenemos:
PAG_solución = (23,8 mm Hg) (0, 947)
PAG_solución = 22,54 mm Hg.

El resultado tiene sentido: en términos moleculares, hay muy poca azúcar disuelta en mucha agua (aunque en términos del mundo real, ambos ingredientes tienen el mismo volumen), por lo que la presión de vapor solo disminuirá ligeramente.

Método 3 de 3: encontrar la presión de vapor en casos especiales

Paso 1. Tenga cuidado con las condiciones de presión y temperatura estándar

Los científicos suelen utilizar un conjunto de valores de temperatura y presión como un "estándar" fácil de usar. Estos valores se denominan temperatura y presión estándar (o STP). Los problemas de presión de vapor a menudo se refieren a condiciones STP, por lo que es importante recordar estos valores. Los valores STP se definen como:

Temperatura: 273, 15 K / 0 C / 32 F
Presión: 760 mm Hg / 1 atm / 101, 325 kilopascales

Paso 2. Reordena la ecuación de Clausius-Clapeyron para encontrar las otras variables

En nuestro ejemplo de la Parte 1, vimos que la ecuación de Clausius-Clapeyron es muy útil para encontrar la presión de vapor de sustancias puras. Sin embargo, no todas las preguntas le pedirán que busque P1 o P2; muchas le pedirán que encuentre el valor de temperatura o, a veces, incluso el valor de H._vapor. Afortunadamente, en estos casos, obtener la respuesta correcta es simplemente una cuestión de reorganizar la ecuación para que las variables que desea resolver estén separadas en un lado del signo igual.

Por ejemplo, digamos que tenemos un líquido desconocido con una presión de vapor de 25 torr a 273 K y 150 torr a 325 K, y queremos encontrar la entalpía de vaporización de este líquido (ΔH_vapor). Podemos resolverlo así:
ln (P1 / P2) = (ΔH_vapor/ R) ((1 / T2) - (1 / T1))
(ln (P1 / P2)) / ((1 / T2) - (1 / T1)) = (ΔH_vapor/ R)
R × (ln (P1 / P2)) / ((1 / T2) - (1 / T1)) = H_vapor Ahora, ingresamos nuestros valores:
8, 314 J / (K × Mol) × (-1, 79) / (- 0, 00059) = H_vapor
8, 314 J / (K × Mol) × 3033, 90 = H_vapor = 25.223, 83 J / mol

Paso 3. Calcule la presión de vapor del soluto cuando la sustancia produce vapor

En nuestro ejemplo de la Ley de Raoult anterior, nuestro soluto, el azúcar, no ejerce ninguna presión por sí solo a temperaturas normales (piense, ¿cuándo fue la última vez que vio evaporarse un tazón de azúcar en su armario superior?) Sin embargo, ¿cuándo lo hizo su soluto? evaporarse, esto afectará su presión de vapor. Esto lo explicamos usando una versión modificada de la ecuación de la ley de Raoult: PAG_solución = (P_compuestoX_compuesto) El símbolo sigma (Σ) significa que solo necesitamos sumar todas las presiones de vapor de los diferentes compuestos para obtener nuestra respuesta.

Por ejemplo, digamos que tenemos una solución hecha de dos químicos: benceno y tolueno. El volumen total de la solución es de 12 mililitros (mL); 60 ml de benceno y 60 ml de tolueno. La temperatura de la solución es de 25 ° C y las presiones de vapor de cada uno de estos productos químicos a 25 ° C son 95,1 mm Hg para el benceno y 28,4 mm Hg para el tolueno. Con estos valores, encuentre la presión de vapor de la solución. Podemos hacer esto de la siguiente manera, usando valores estándar de densidad, masa molar y presión de vapor para nuestros dos productos químicos:
Masa (benceno): 60 mL = 0.060 L y veces 876.50 kg / 1,000 L = 0.053 kg = 53 g
Masa (tolueno): 0.060 L y veces 866, 90 kg / 1,000 L = 0.052 kg = 52 g
Mol (benceno): 53 g × 1 mol / 78, 11 g = 0,679 mol
Moles (tolueno): 52 g × 1 mol / 92, 14 g = 0,564 mol
Total de lunares: 0,679 + 0,564 = 1,243
Fracción molar (benceno): 0,679 / 1, 243 = 0,546
Fracción molar (tolueno): 0,564 / 1, 243 = 0,454
Solución: P_solución = P_bencenoX_benceno + P_toluenoX_tolueno
PAG_solución = (95,1 mm Hg) (0, 546) + (28,4 mm Hg) (0, 454)
PAG_solución = 51,92 mm Hg + 12,89 mm Hg = 64, 81 mm Hg

Consejos

Para usar la ecuación de Clausius Clapeyron anterior, la temperatura debe medirse en Kelvin (escrito como K). Si tiene la temperatura en grados Celsius, debe convertirla usando la siguiente fórmula: T_k = 273 + T_C
Los métodos anteriores se pueden utilizar porque la energía es exactamente proporcional a la cantidad de calor aplicada. La temperatura del líquido es el único factor ambiental que afecta la presión de vapor.