- Autor Jason Gerald [email protected].
- Public 2023-12-16 11:06.
- Última modificación 2025-01-23 12:16.
Si ya lo entiende, convertir fracciones ordinarias a decimales no es difícil. Para convertir fracciones comunes en decimales, puede usar la división larga, la multiplicación o incluso una calculadora si no desea calcular a mano. Una vez que domine el método, podrá convertir fracciones a decimales fácilmente.
Paso
Método 1 de 4: con división larga
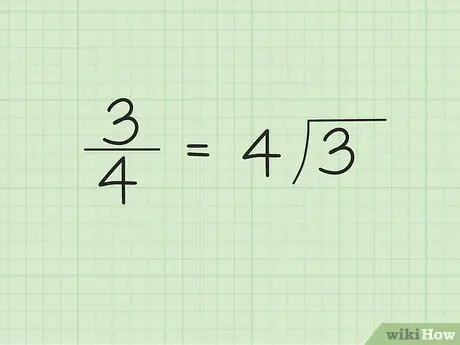
Paso 1. Escriba el denominador fuera / lado izquierdo del símbolo divisor y el numerador dentro / lado derecho del símbolo divisor
Por ejemplo, digamos que queremos convertir 3/4 a decimal. Escriba "4" fuera / lado izquierdo del símbolo del divisor y "3" dentro / lado derecho del símbolo del divisor. "4" es el número que divide y "3" es el número que se divide.

Paso 2. Escriba "0", luego un punto decimal (una coma), encima del símbolo del divisor
Dado que lo que cuenta es una fracción, el resultado debe ser menor que uno, por lo que este paso es muy importante. Después de eso, escriba el signo decimal, luego "0", después del número "3" en el lado derecho del símbolo del divisor. Aunque "3" es igual a "3, 0", el cero permite dividir "3, 0" por "4".

Paso 3. Calcula la respuesta usando una división larga
Con la división larga, por ahora, el signo decimal se puede ignorar, por lo que solo necesita calcular 30 dividido por 4. Así es como:
- Primero, divide 3, 0, que cuenta como 30, entre 4. El 4 más cercano a 30 es 4 x 7 = 28, dejando 2. Entonces, escribe “7” después de “0” encima del divisor y “28” debajo de “3, 0”en / lado derecho del símbolo del divisor. Menores de 28, escriba "2", el resto de 30 menos 28.
- A continuación, escriba "0" después de "3, 0" para que se convierta en "3, 00", que se puede considerar como "300", dentro / lado derecho del símbolo del divisor. Por lo tanto, se puede bajar 0 a la derecha de "2" para que "20" sea divisible por "4".
- “20” dividido por “4” es igual a “5”. Por lo tanto, escriba "5" después de "0,7" sobre el símbolo del divisor para que se convierta en "0,75".

Paso 4. Escribe la respuesta final
Entonces, "3" dividido por "4" es igual a "0,75". Escriba la respuesta. Finalizado.
Método 2 de 4: Fracciones que generan decimales repetidos
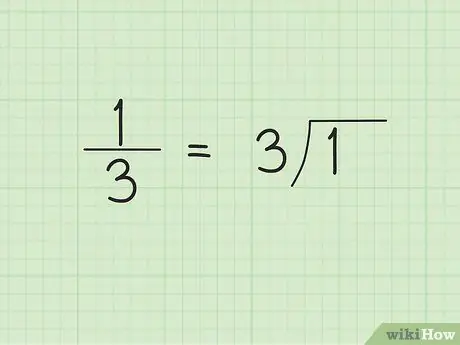
Paso 1. Haz una división de división larga
Cuando comience la división de dígitos largos, es posible que no pueda predecir que el resultado será un número decimal periódico. Por ejemplo, digamos que queremos convertir la fracción común 1/3 a forma decimal. Escribe 3, o el denominador, en el lado exterior / izquierdo del símbolo del divisor y 1 dentro / lado derecho del símbolo del divisor.

Paso 2. Escribe un 0, luego un signo decimal, encima del símbolo del divisor
Dado que el resultado debe ser menor que 1, este paso prepara la respuesta para ser escrita en forma decimal. El signo decimal también debe escribirse a la derecha del número "1" que se encuentra en el lado derecho del símbolo divisor.
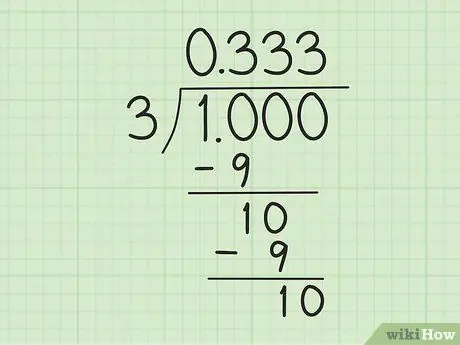
Paso 3. Comience a calcular la división de división larga
Empiece por convertir "1" en "1, 0", que cuenta como "10", por lo que es divisible por "3". A continuación, realice los siguientes pasos:
- Dividir 10 entre 3. Usa 3 x 3 = 9 para hacer un resto de 1. Así que escribe 3 a la derecha del “0”, encima del símbolo del divisor y resta 10 por 9 para obtener un resto de 1.
- Escriba un "0" a la derecha del número "1" (el resto de 10 menos 9 en el paso anterior) a continuación para obtener otro "10". Al dividir nuevamente “10” por “3”, se repite el mismo proceso: escriba “3” a la derecha del primer “3” encima del símbolo divisor y reste el nuevo “10” por “9”.
- Continúe hasta que se forme un patrón. ¿Sabes que algo es raro? Esta división puede durar para siempre. 10 siempre es divisible por 3: siempre habrá un "1" en la parte inferior y un nuevo "3" después del decimal sobre el símbolo del divisor.
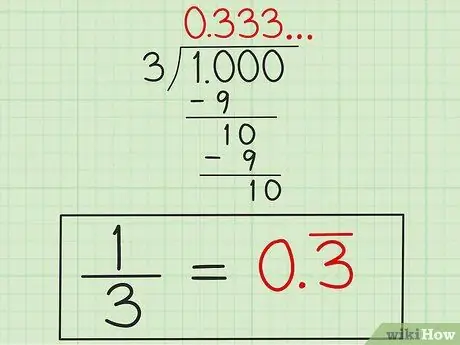
Paso 4. Escribe la respuesta
Después de saber que "3" se repetirá, escriba la respuesta como "0, 3" con una línea sobre el número "3" (o "0, 33" con una línea sobre ambos números "3") como una indicación de que el número "3" se sigue repitiendo. Esta respuesta está en forma decimal 1/3 porque 1 dividido por 3 no terminará solo.
Hay muchas fracciones que producen decimales repetidos, como 2/9 ("0, 2" con "2" repetido), 5/6 ("0, 83" con "3" repetido) o 7/9 ("0, 7”con“7”sigue repitiéndose). Este patrón siempre ocurre cuando el denominador es un múltiplo de 3 y el numerador no puede ser divisible por el denominador
Método 3 de 4: por multiplicación

Paso 1. Encuentra el número que se puede multiplicar por el denominador de la fracción para producir 10, 100, 1,000 o cualquier número que sea base 10
Esta puede ser una manera fácil de convertir fracciones a decimales sin usar una división larga o una calculadora. Primero, solo encuentra un número que se pueda multiplicar por el denominador de la fracción para obtener 10, 100, 1,000, etc. Para hacer esto, primero divida 10, luego 100, luego 1,000, y así sucesivamente por el denominador hasta obtener un número entero. Ejemplo:
- 3/5. 10/5 = 2,2 es un número entero. 2 se puede multiplicar por 5 para hacer 10. Por lo tanto, se puede usar 2.
- 3/4. 10/4 = 2, 5. 2, 5 no es un número entero. 100/4 = 25. 25 es un número entero. 25 se puede multiplicar por 4 para hacer 100. Por lo tanto, se puede usar 25.
- 5/16. 10/16 = 0, 625, 100/16 = 6, 25, 1,000 / 16 = 62, 5, 10,000 / 16 = 625. 625 es el primer número entero obtenido. 625 se puede multiplicar por 16 para obtener 10,000. Entonces, se puede usar 625.
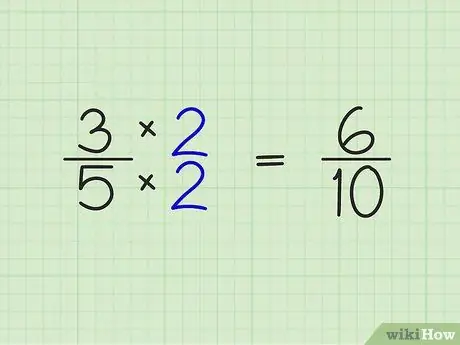
Paso 2. Multiplica el numerador y el denominador de la fracción por el número entero obtenido en el paso anterior
Este paso es bastante sencillo. Simplemente multiplica los números arriba y abajo de la fracción por el número entero que obtuviste en el paso anterior. Ejemplo:
- 3/5 x 2/2 = 6/10
- 3/4 x 25/25 = 75/100
- 5/16 x 625/625 = 3,125 / 10000

Paso 3. Escribe la respuesta final
La respuesta es que el numerador está marcado con un decimal de acuerdo con el número de ceros en el denominador. Solo cuenta cuántos ceros hay en el denominador. Si solo hay 1 0 en el denominador, mueva el punto decimal 1 dígito hacia la izquierda y así sucesivamente. Ejemplo:
- 3/5 = 6/10 = 0, 6
- 3/4 = 75/100 = 0, 75
- 5/16 = 3.125/10.000 = 0, 3125
Método 4 de 4: con calculadora

Paso 1. Divida el numerador por el denominador
Este método es muy sencillo. Simplemente use una calculadora para dividir el numerador, el número en la parte superior de la fracción, por el denominador, el número en la parte inferior de la fracción. Por ejemplo, supongamos que desea convertir 3/4 a decimal. Simplemente presione "3", luego el símbolo de división ("÷ '"), luego "4", y finalmente el símbolo de igual ("=").

Paso 2. Escriba las respuestas que obtenga
La respuesta es 0,75, por lo que la forma decimal de la fracción común 3/4 es 0,75.
Consejos
- Para comprobar si su respuesta es correcta, multiplique la respuesta por el denominador de la fracción. Si tu respuesta es correcta, el producto de la multiplicación es el numerador de la fracción.
- Algunas fracciones se pueden convertir a decimales creando fracciones comparables cuyos denominadores sean base 10 (10, 100, 1,000, etc.). Luego, use valores posicionales para escribir la forma decimal correcta.






