- Autor Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-16 19:22.
- Última modificación 2025-01-23 12:16.
Al estudiar instrumentos ópticos, el "aumento" de un objeto similar a una lente es la relación entre la altura de la imagen que ve y la altura real del objeto. Por ejemplo, una lente que puede hacer que un objeto parezca muy grande tiene un factor de aumento "alto", mientras que una lente que hace que un objeto parezca pequeño tiene un factor de aumento "bajo". La fórmula para la ampliación de un objeto generalmente se calcula usando la fórmula M = (hI/ ho) = - (dI/Do), donde M = aumento, hI = altura de la imagen, ho = altura del objeto, ydI y Do = distancia de la imagen y el objeto.
Paso
Método 1 de 2: Cálculo de la ampliación de una sola lente
Notas: A lentes convergentes más ancho en el centro que en los bordes (como una lupa). a lente divergente más ancho en los bordes que en el centro (como un cuenco). El cálculo de la ampliación en ambas lentes es el mismo, con una excepción importante. Haga clic aquí para ir directamente a las excepciones a lentes divergentes.
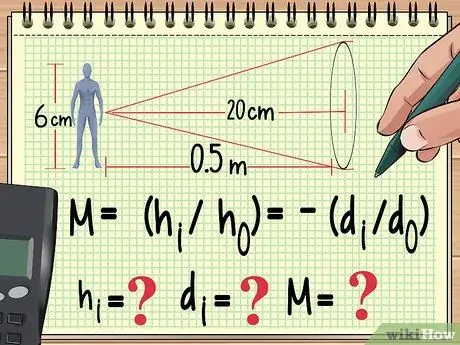
Paso 1. Empiece con su ecuación y las variables que ya conoce
Al igual que con cualquier otro problema de física, la forma de resolver un problema de ampliación es escribir la ecuación que utilizará para calcularlo. Desde aquí, puede trabajar hacia atrás para encontrar el valor de la variable que no ha encontrado en la ecuación que está usando.
-
Por ejemplo, suponga que una muñeca de 6 cm de altura se coloca a un metro de una lentes convergentes con una distancia focal de 20 cm. Si queremos calcular el aumento, la altura de la imagen y la distancia de la imagen, podemos comenzar a escribir nuestra ecuación de la siguiente manera:
-
- M = (hI/ ho) = - (dI/Do)
-
- Ahora sabemos ho (altura de la muñeca) ydo (distancia de la muñeca a la lente). También conocemos la distancia focal de la lente, que no está en esta ecuación. Contaremos hI, DI, y M.

Paso 2. Usando la ecuación de la lente para obtener dI.
Si conoce la distancia desde el objeto que está ampliando y la distancia focal de la lente, calcular la distancia desde la imagen formada es muy fácil con la ecuación de la lente. La ecuación de la lente es 1 / f = 1 / do + 1 / díaI, donde f = distancia focal de la lente.
-
En este problema de ejemplo, podemos usar la ecuación de la lente para calcular dI. Ingrese los valores de fydI luego resuelve la ecuación:
-
- 1 / f = 1 / do + 1 / díaI
- 1/20 = 1/50 + 1 / díaI
- 5/100 - 2/100 = 1 / díaI
- 3/100 = 1 / díaI
- 100/3 = dI = 33,3 cm
-
- La distancia focal de la lente es la distancia desde el centro de la lente hasta el punto donde se transmite la luz en el punto focal. Si alguna vez ha enfocado la luz con una lupa en hormigas en llamas, lo ha visto. En las preguntas de la lección, generalmente se ha dado la magnitud de este punto de acceso. En la vida real, estas especificaciones suelen estar escritas en una etiqueta ubicada en la lente.

Paso 3. Calcular hI.
Después de calcular do y DI, puede calcular la altura del objeto ampliado y el aumento de la lente. Observe los dos signos iguales en la ecuación de aumento de la lente (M = (hI/ ho) = - (dI/Do)) - esto significa que todas las partes de esta ecuación son iguales entre sí, por lo que podemos calcular M y hI en el orden que queramos.
-
Para este problema de ejemplo, podemos calcular hI como esto:
-
- (hI/ ho) = - (dI/Do)
- (hI/6) = -(33, 3/50)
- hI = - (33, 3/50) x 6
- hI = - 3, 996 cm
-
- Tenga en cuenta que la altura del objeto aquí es negativa lo que indica que la imagen que veremos más adelante estará invertida (de arriba a abajo).

Paso 4. Cálculo de M
Puedes calcular la última variable con la ecuación - (dI/Do) o (hI/ ho).
-
En el siguiente ejemplo, cómo calcular M es el siguiente:
-
- M = (hI/ ho)
-
M = (-3, 996/6) = - 0, 666
-
-
El resultado también será el mismo cuando se calcule utilizando el valor de d:
-
- M = - (dI/Do)
- M = - (33, 3/50) = - 0, 666
-
- Tenga en cuenta que el zoom no tiene una etiqueta de unidad.
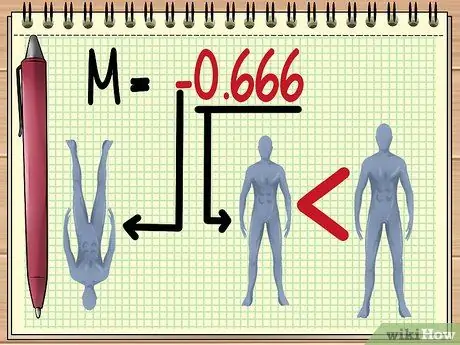
Paso 5. Comprensión del valor M
Una vez que obtenga la magnitud del valor M, puede estimar varias cosas sobre la imagen que verá a través de la lente, a saber:
-
El tamaño.
Cuanto mayor sea el "valor absoluto" de M, más grande aparecerá el objeto visto con la lente. El valor de M entre 0 y 1 indica que el objeto se verá más pequeño.
-
Orientación a objetos.
Un valor negativo indica que la imagen formada se invertirá.
- En el ejemplo dado aquí, el valor M de -0,666 significa que, según el valor de la variable existente, la sombra del muñeco será visible. al revés y dos tercios más pequeño que el tamaño real.
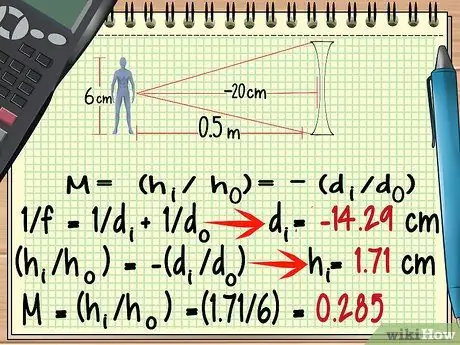
Paso 6. Para una lente divergente, use un punto focal negativo
Aunque la forma de una lente divergente es muy diferente a la de una lente convergente, puede calcular su aumento utilizando la misma fórmula anterior. Las excepciones a tener en cuenta son El punto focal de la lente divergente es negativo.
En el problema de ejemplo anterior, esto afectará la respuesta que obtendrá al calcular dI, así que asegúrate de prestar atención a esto.
-
Repasemos el problema de ejemplo anterior, solo que ahora usamos una lente divergente con distancia focal - 20 centímetros.
Las otras variables siguen teniendo el mismo valor.
-
En primer lugar, calcularemos dI usando la ecuación de la lente:
-
- 1 / f = 1 / do + 1 / díaI
- 1 / -20 = 1/50 + 1 / dI
- -5/100 - 2/100 = 1 / díaI
- -7/100 = 1 / díaI
- -100/7 = dI = - 14, 29 cm
-
-
Ahora calcularemos hI y M con un valor de dI el nuevo.
-
- (hI/ ho) = - (dI/Do)
- (hI/6) = -(-14, 29/50)
- hI = - (- 14, 29/50) x 6
- hI = 1, 71 cm
- M = (hI/ ho)
- M = (1, 71/6) = 0, 285
-
Método 2 de 2: cálculo de la ampliación de varios objetivos
Método simple de dos lentes
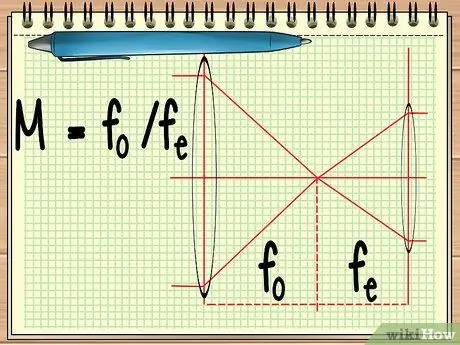
Paso 1. Calcule el punto focal de las dos lentes
Cuando utiliza un instrumento que consta de dos lentes dispuestos uno al lado del otro (como un telescopio o un par de binoculares), todo lo que tiene que averiguar es el punto focal de los dos lentes para calcular el aumento total de los dos lentes. esto se puede calcular mediante la ecuación simple M = fo/Fmi.
En la ecuación, fo es el punto focal de la lente del objetivo yfmi es el punto focal del ocular. La lente del objetivo es la lente grande que está cerca del objeto, mientras que la lente ocular es la lente que está ubicada cerca del ojo del observador.

Paso 2. Inserta la información que ya tienes en la ecuación M = fo/Fmi.
Una vez que tenga los puntos focales de ambas lentes, es muy fácil calcularlos; calcule la relación dividiendo la distancia focal de la lente del objetivo por la distancia focal del ocular. La respuesta que obtiene es el aumento total de la herramienta.
-
Por ejemplo, suponga un telescopio simple, está escrito que el punto focal de la lente del objetivo es de 10 cm y el punto focal del ocular es de 5 cm, entonces el aumento es 10/5 = 2.
Método complicado
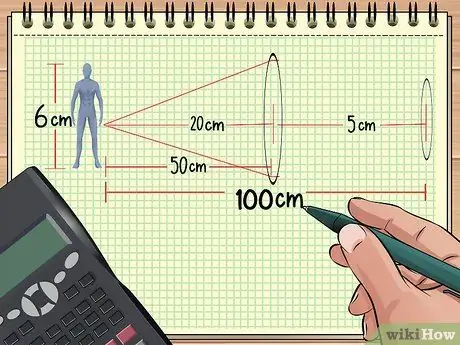
Paso 1. Calcula la distancia entre las lentes y el objeto
Si tiene dos lentes dispuestos en una fila frente a un objeto, el aumento total se puede calcular si conoce la distancia entre los lentes y el objeto, el tamaño del objeto y el punto focal de los dos lentes. El resto también se puede calcular.
Por ejemplo, supongamos que colocamos objetos y lentes como en el problema de ejemplo 1 anterior: una muñeca está a 50 cm de una lente convergente que tiene una distancia focal de 20 cm. Ahora, coloca la segunda lente con punto focal a 5 cm a una distancia de 50 cm de la primera lente (a 100 cm de la muñeca). Después de esto, calcularemos el aumento total con la información que hemos obtenido
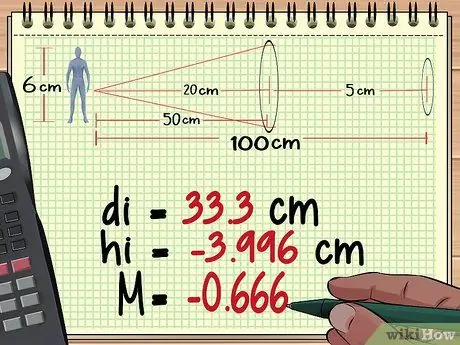
Paso 2. Calcule la distancia, la altura y el aumento del objeto desde la lente 1
La primera parte del cálculo del aumento de múltiples lentes es lo mismo que calcular el aumento de un solo lente. Comience con la lente más cercana al objeto, use la ecuación de la lente para encontrar la distancia desde la imagen formada, luego use la ecuación de aumento para encontrar la altura y el aumento de la imagen. Haga clic aquí para ver más cálculos de aumento de lente única.
-
De nuestros cálculos en el Método 1 anterior, encontramos que la primera lente produce una imagen tan alta como - 3, 996 cm, distancia 33,3 cm detrás de la lente, y con un aumento de - 0, 666.
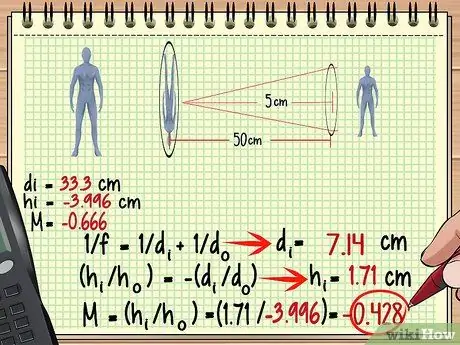
Paso 3. Utilice la imagen de la primera lente como el objeto de la segunda lente
Ahora, encontrar el aumento, la altura y más para la segunda lente es muy fácil: solo use el mismo método que usó para la primera lente, solo, esta vez trate la imagen como un objeto. Recuerde que la distancia de la imagen a la segunda lente no siempre es la misma que la distancia del objeto a la primera lente.
-
En el ejemplo anterior, dado que la imagen se forma a 33,3 cm detrás de la primera lente, la distancia es 50-33,3 = 16,7 cm delante de la segunda lente. Usemos esta medida y la distancia focal de la segunda lente para encontrar la imagen formada por la segunda lente.
-
- 1 / f = 1 / do + 1 / díaI
- 1/5 = 1/16, 7 + 1 / díaI
- 0, 2 - 0, 0599 = 1 / dI
- 0, 14 = 1 / díaI
- DI = 7, 14 cm
-
-
Ahora podemos calcular hI y M para la segunda lente:
-
- (hI/ ho) = - (dI/Do)
- (hI/-3, 996) = -(7, 14/16, 7)
- hI = - (0, 427) x -3, 996
- hI = 1, 71 cm
- M = (hI/ ho)
- M = (1, 71 / -3, 996) = - 0, 428
-
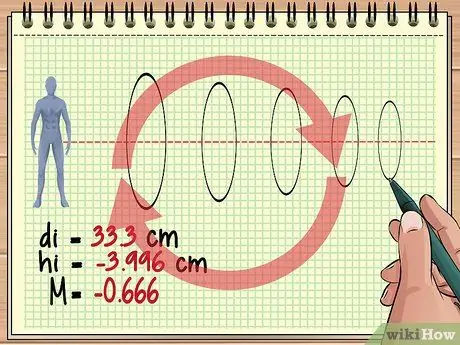
Paso 4. Continúe calculando así para las lentes adicionales
Este enfoque básico es el mismo si hay tres, cuatro o cientos de lentes alineados frente a un objeto. Para cada lente, considere la imagen de la lente anterior como el objeto y use la ecuación de la lente y la ecuación de aumento para encontrar la respuesta que desea.
Tenga en cuenta que cada lente posterior puede invertir continuamente la imagen formada. Por ejemplo, el valor de aumento que obtuvimos anteriormente (-0, 428) indica que la imagen que vamos a ver es aproximadamente 4/10 del tamaño real del objeto, pero perpendicular, porque la imagen de la lente anterior está invertida
Consejos
- Los binoculares suelen proporcionar una explicación de las especificaciones de aumento en forma de un número multiplicado por otro número. Por ejemplo, los prismáticos se pueden especificar como 8x25 u 8x40. Cuando se escribe así, el primer número es el aumento de los binoculares. No importa incluso si en el ejemplo dado, los dos números son diferentes en magnitud, ambos binoculares tienen un aumento de 8 veces. El segundo número indica qué tan clara será la imagen formada por los binoculares.
- Recuerde que para las lupas de un solo objetivo, el aumento será negativo si la distancia del objeto es mayor que la distancia focal del objetivo. Esto no significa que la imagen formada sea más pequeña. En este caso, la ampliación todavía se produce, pero el observador verá la imagen formada al revés (de arriba hacia abajo).






