Siempre que sepas la medida de los otros dos ángulos, es fácil encontrar el tercer ángulo de un triángulo. Solo necesitas restar 180 grados la suma de los dos ángulos. Sin embargo, también hay otras formas que puede utilizar para encontrar el tercer ángulo de un triángulo si la forma del problema es un poco diferente de lo habitual. Si desea saber cómo encontrar el tercer ángulo de un triángulo, siga la guía a continuación.
Paso
Método 1 de 3: Usar las medidas de los otros dos ángulos
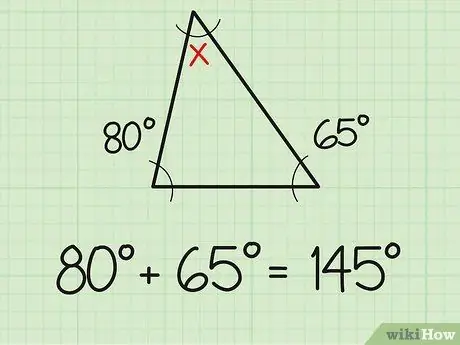
Paso 1. Sume los dos ángulos conocidos
Un dato que debes saber es que la suma de los tres ángulos de un triángulo es siempre 180 grados. Entonces, si ya conoces la medida de los dos ángulos de un triángulo, encontrar el tercer ángulo será tan simple como resolver problemas simples de suma y resta. Primero, suma las dos medidas de los ángulos que ya conoces. Por ejemplo, dos ángulos conocidos miden 80 y 65 grados. Suma los dos (80 + 65) y obtienes 145 grados.
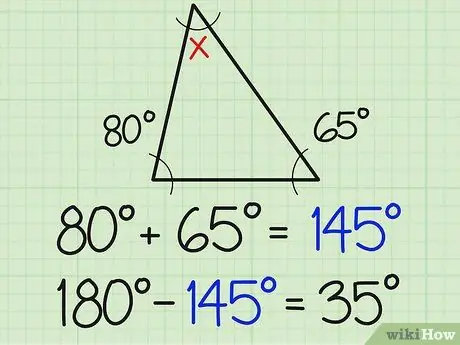
Paso 2. Divida ese número por 180
La suma de los tres ángulos de un triángulo es siempre 180 grados. Por lo tanto, el tercer ángulo debe ser 180 cuando se suma a la suma de las dos medidas conocidas del ángulo. En el ejemplo anterior, esto significa 180-154 = 35.
Paso 3. Escribe tu respuesta
Ahora tienes la respuesta al tercer ángulo (en el ejemplo 35 grados). Si aún tiene dudas, compruébelo usted mismo. Suma los tres ángulos y obtendrás un resultado de 180. Si no lo haces, tu cálculo es incorrecto. Para este ejemplo, 80 + 65 + 35 = 180. Si es correcto, significa que ha resuelto el problema.
Método 2 de 3: uso de variables
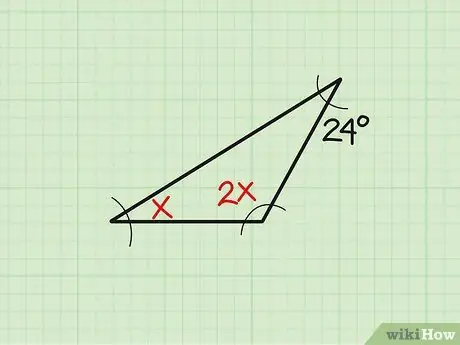
Paso 1. Anote el problema
A veces, el tamaño del ángulo existente se muestra en forma variable. Tomemos este ejemplo: "Encuentra el ángulo" x "de un triángulo si los tres ángulos miden" x "," 2x "y 24, respectivamente". Primero, anote el problema.
Paso 2. Sume todas las medidas de los ángulos
El principio que debes recordar sigue siendo el mismo. Entonces, primero sume los tres ángulos del problema, a saber, "x + 2x + 24 = 3x + 24".
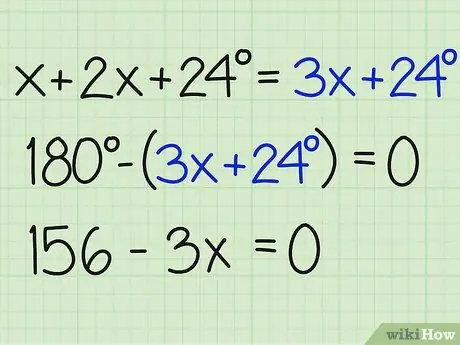
Paso 3. Divide la suma de los ángulos por 180
Ahora, diferencia ese número en 180 grados para encontrar xy averigua la respuesta al problema. Asegúrate de terminar la ecuación igual a cero. Así es como está escrito:
- 180- (3x + 24) = 0
- 180-3x-24 = 0
- 156-3x = 0
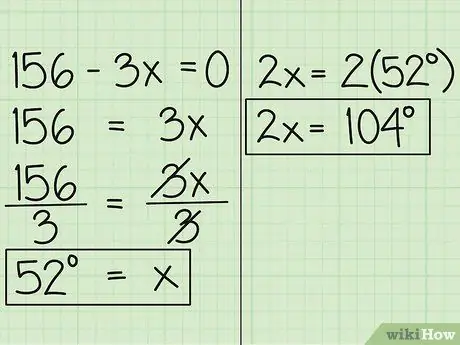
Paso 4. Encuentra el valor de x
Ahora, mueva la variable al otro lado de la ecuación y obtendrá 156 = 3x. Luego, divide la ecuación por 3, de modo que obtengas x = 52. Esto significa que la medida del ángulo expresado en x es 52 grados. El otro ángulo, expresado en 2x es 52 grados por 2, que es 104 grados.
Paso 5. Verifique sus resultados
Si desea asegurarse de que su respuesta sea correcta, simplemente sume las tres medidas de los ángulos a las que ya encontró la respuesta. Si el resultado es 180, significa que su respuesta es correcta. Para este ejemplo, 52 + 104 + 24 = 180.
Método 3 de 3: Usar otros métodos
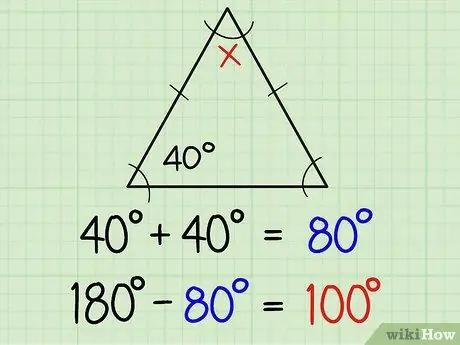
Paso 1. Encuentra los ángulos de un triángulo isósceles
Un triángulo isósceles tiene dos lados iguales y dos ángulos iguales. Por lo general, dos lados iguales se marcan con una pequeña línea en el medio de la línea lateral, lo que significa que los dos ángulos opuestos de la línea tienen la misma medida. Si ya conoce el tamaño de un ángulo, automáticamente conoce el otro ángulo. Aquí hay una explicación más detallada:
Si uno de los ángulos iguales es de 40 grados, el otro es de 40 grados. De esa manera, puede encontrar los tres ángulos con la diferencia entre la suma de 40 + 40 (es decir, 80) y 180, o en otras palabras, 180-80 = 100
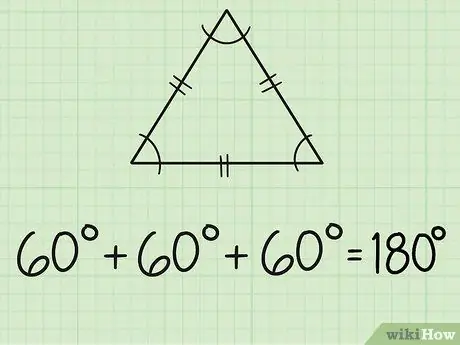
Paso 2. Encuentra los ángulos de un triángulo equilátero
Un triángulo equilátero tiene tres lados iguales y tres ángulos iguales. Cada lado suele estar marcado con dos líneas cortas en el medio. Dado que los tres ángulos son iguales, significa que todos los ángulos miden 60 grados, porque 180/3 = 60.
Paso 3. Encuentra el tercer ángulo en un triángulo rectángulo
Suponga que obtiene un triángulo rectángulo, con uno de los ángulos agudos que mide 30 grados. Dado que el triángulo es un ángulo recto, significa que uno de los ángulos, es decir, el ángulo recto, debe medir 90 grados. Luego usa el principio del triángulo, la diferencia entre la suma de los dos ángulos (90 + 30 = 120) por 180, entonces obtendrás 180-120 = 60 grados.
