- Autor Jason Gerald [email protected].
- Public 2024-01-19 22:12.
- Última modificación 2025-01-23 12:16.
Las bolas de billar chocan entre sí con perfecta elasticidad. Es decir, la energía cinética del movimiento se conserva casi por completo y muy poca de ella se convierte en calor u otra energía. Esto hace que el billar sea un deporte interesante para analizar matemáticamente. Si tiene un control total sobre cómo empuja la bola blanca y hacia dónde va, siempre podrá predecir lo que sucederá.
Paso
Parte 1 de 3: Predecir el ángulo de rebote de la pelota en el carril
Paso 1. Comprender la ley de la reflexión
Muchos jugadores de billar ya conocen esta simple matemática porque es necesaria cada vez que quieren hacer rebotar la pelota en los rieles (bordes acolchados en la mesa de billar). Esta ley establece que el ángulo de incidencia de la reflexión es igual al ángulo de salida. Es decir, si la pelota golpea la barandilla en un ángulo de 30º, el ángulo de rebote también será de 30º.
La ley de la reflexión se refería originalmente a la naturaleza de la luz. Por lo general, esta ley dice "El ángulo de incidencia es igual al ángulo de reflexión"
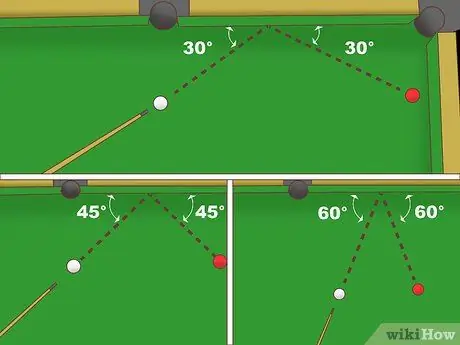
Paso 2. Coloque la bola blanca y la bola objetivo a la misma distancia del riel
En este escenario, su objetivo es hacer rebotar la bola blanca en la barandilla y golpear la bola objetivo. Ahora, intente aplicar las siguientes técnicas geométricas básicas:
- Dibuja una línea de sombra desde la bola blanca que es perpendicular al riel. Esta es la primera línea.
- Luego, imagina la trayectoria del reflejo de la bola blanca hacia la barandilla. Esta línea es la hipotenusa (hipotenusa) de un triángulo rectángulo formado por la primera línea y el carril.
- Ahora, imagina la bola blanca rebotando en la barandilla y golpeando la bola objetivo. Suponga que hay un segundo triángulo rectángulo en la esfera del objeto que es simétrico al primer triángulo.
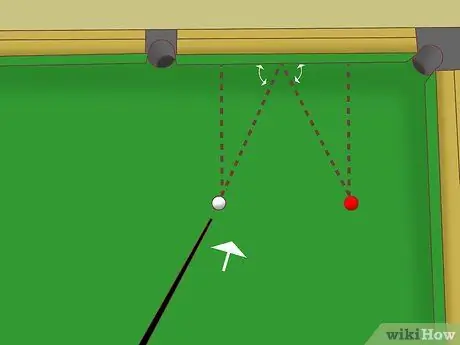
Paso 3. Demuestra que estos dos triángulos son congruentes
En este caso, podemos usar la regla "Ángulo lateral". Si ambos triángulos tienen dos ángulos iguales y un lado es el mismo (en la misma configuración), entonces los dos triángulos son congruentes. (En otras palabras, la forma y el tamaño son iguales). Podemos probar si estos dos triángulos en la mesa de billar cumplen estas condiciones:
- La ley de la reflexión establece que los dos ángulos entre la hipotenusa y el carril tienen la misma medida.
- Ambos son ángulos rectos, por lo que cada uno tiene un ángulo de 90º.
- Dado que las dos bolas están a la misma distancia del riel, los dos lados entre la bola y el riel tienen la misma longitud.
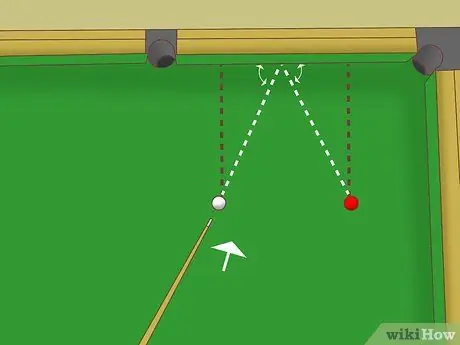
Paso 4. Apunte al punto medio del riel
Dado que estos dos triángulos son congruentes, las longitudes de los lados de los rieles también son iguales entre sí. Es decir, la distancia desde el punto de rebote hasta las dos bolas es la misma. Apunta al punto medio si la bola blanca y la bola objetivo están a la misma distancia de la banda.
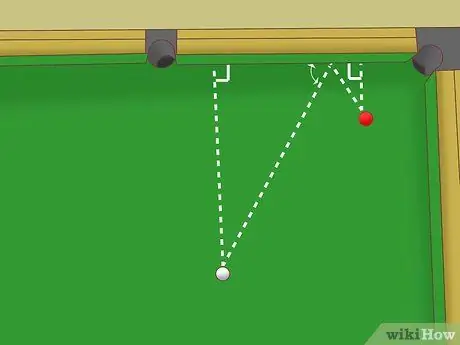
Paso 5. Utilice un triángulo similar si la bola blanca y la bola objetivo no están a la misma distancia de la barandilla
Digamos que la distancia de la bola blanca a la barandilla es el doble de la distancia de la bola objetivo a la barandilla. Todavía puedes imaginar los dos triángulos rectángulos formados por el camino ideal de la esfera blanca y usar tu intuición geométrica para apuntar:
- Los dos triángulos todavía tienen los mismos ángulos, pero diferentes longitudes de lado. Es decir, los dos triángulos siguen siendo similares: la forma es la misma, pero el tamaño es diferente.
- Dado que la bola blanca está dos veces más lejos de la barandilla, el primer triángulo es dos veces más grande que el segundo triángulo.
- Es decir, el lado del riel del primer triángulo es dos veces más largo que el lado del riel del segundo triángulo.
- En este caso, apunte a un punto en la barandilla a la distancia de la bola objetivo porque es dos veces.
Parte 2 de 3: Cálculo del ángulo de impacto de los objetos de bola
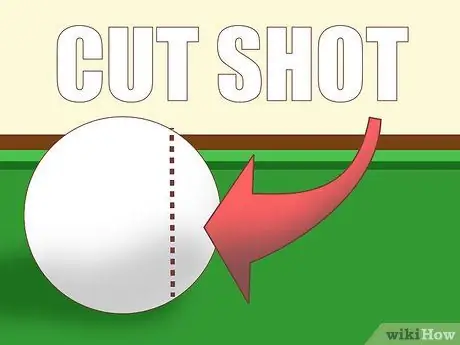
Paso 1. Aprenda los conceptos básicos
La mayoría de los golpes en el billar son tiros de esquina o "cortes", lo que significa que la bola blanca no golpea el objeto directamente. Cuanto más "delgada" golpee la bola, mayor será el ángulo de trayectoria de la bola del objeto, dependiendo de la trayectoria de la bola blanca.
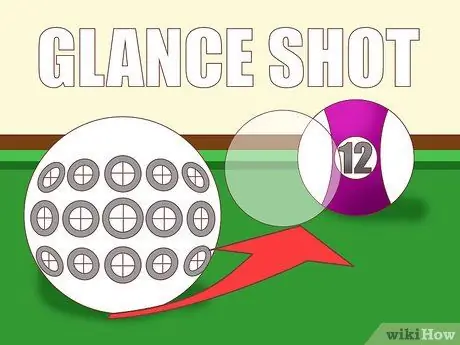
Paso 2. Estime la plenitud del impacto
Una buena forma de estimar este efecto es monitorear el impacto contra la trayectoria planificada de la pelota. Cuando las bolas chocan, ¿cuánto se "superpone" la bola blanca a la bola objeto desde su perspectiva? La respuesta mostrará qué tan "lleno" golpeó la pelota:
- Los muertos se superponen completamente. Se podría decir que el nivel de "plenitud" es 1.
- Si la bola blanca cubre las bolas del objeto, significa que la colisión de las bolas está completa.
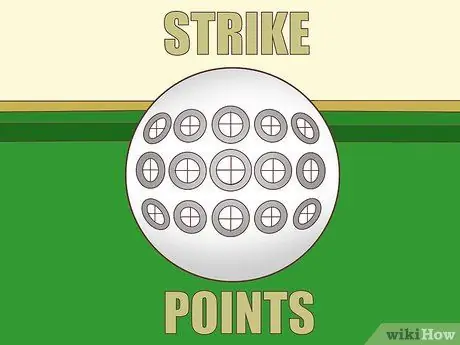
Paso 3. Calcule el ángulo según el grado de plenitud
Las gráficas de estas dos cantidades no son del todo lineales, pero lo suficientemente cercanas como para que pueda estimarlas sumando 15º cada vez que resta la plenitud. De lo contrario, puede utilizar las siguientes medidas que son más precisas:
- El impacto directo (primer grado de plenitud) da como resultado un ángulo de corte de 0º. La bola objetivo continúa completamente el camino de la bola blanca.
- Un impacto completo envía la bola objetivo en un ángulo de 14,5º.
- Un impacto completo envía la bola objetivo en un ángulo de 30º.
- Una colisión completa envía la bola objetivo en un ángulo de 48, 6º.
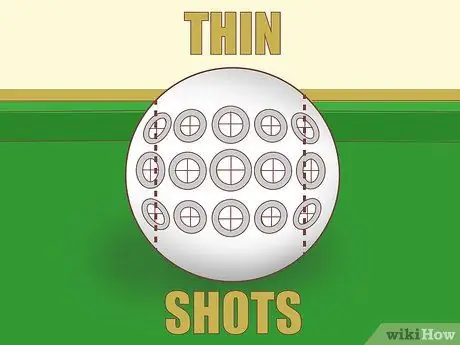
Paso 4. Tenga cuidado al disparar con poco espesor
Si desea golpear la pelota con una plenitud menor a, es difícil estimar el número de bolas cubiertas. Además, el impacto del ángulo de corte es tan drástico que un pequeño error cambiará en gran medida el ángulo resultante. Este tiro tangente requiere mucha práctica y funciona bien una vez que sabes el punto al que estás apuntando. Si puede, busque otra toma para tomar.
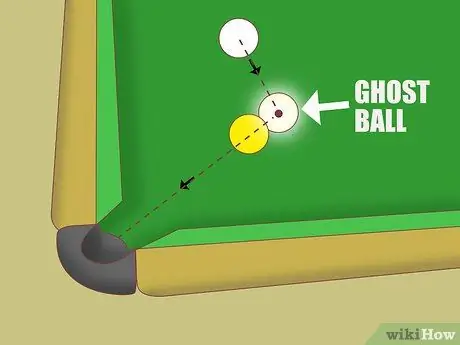
Paso 5. Intente aplicar el método de la bola fantasma para apuntar
Si la descripción de la amplitud del impacto no le ayuda, pruebe el enfoque de "bola fantasma":
- Imagina que hay una línea recta desde el bolsillo de la mesa hasta el centro de la bola objetivo.
- Extienda esta línea un poco más allá de la bola objeto. Imagina que hay una "bola fantasma" en este punto, estando en la línea y tocando la bola objetivo.
- Para golpear la bola objetivo en la tronera, debes apuntar al centro de la "bola fantasma".
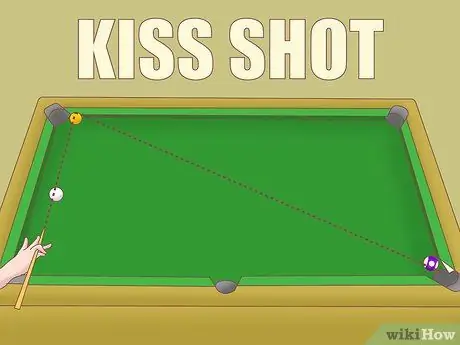
Paso 6. Aplique la tercera regla de las inyecciones de beso
Un golpe de picoteo se realiza golpeando una bola blanca contra la bola A para que apunte y golpee la bola B. Si estás jugando un juego en el que se permiten besos, ten en cuenta esta regla: si la bola A golpea la banda, el ángulo de corte al que apunta es el ángulo formado por las tres bolas.
Por ejemplo, si el ángulo con la esfera A como vértice es de 45º, el ángulo de corte es de unos 15º. La regla de plenitud anterior establece que este ángulo se puede producir con una colisión total
Parte 3 de 3: Uso del inglés (giro lateral)
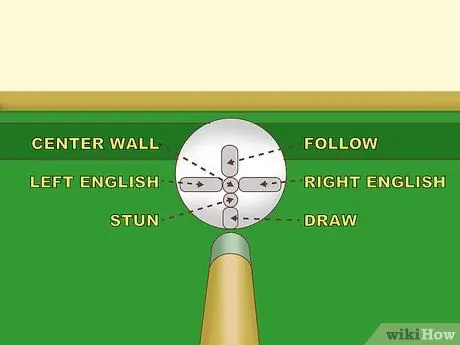
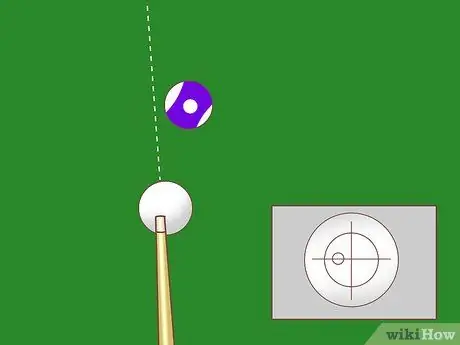
Paso 1. Primero perfecciona tu golpe
Un golpe con una actitud y un objetivo consistentes debe ser una prioridad si quieres jugar al billar en serio. El inglés es una técnica muy útil, pero sus efectos son complejos y debes practicarlo de manera constante.
Te resultará difícil reducir el impacto del inglés si no tomas el control de las fuerzas de deslizamiento y desbordamiento. Este impacto está determinado por la altura del punto de empuje de la pelota. El deslizamiento se puede eliminar por completo golpeando un punto del largo entre el centro y la parte superior de la pelota, pero es común que los jugadores golpeen en un punto a esta distancia para un control y velocidad óptimos
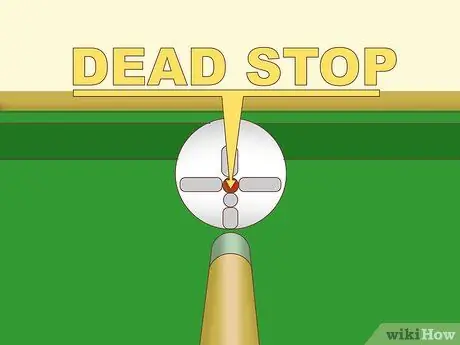
Paso 2. Manténgase alejado del inglés cuando la bola blanca esté en peligro de entrar en la bolsa
Siempre que no haya inglés, la bola blanca se detendrá por completo después de un impacto directo perfecto. Practica el impacto directo golpeando exactamente el centro de los ejes vertical y horizontal de la bola blanca. Una vez que consigas que la bola blanca se detenga por completo cada vez, deberás tener la habilidad suficiente para incluir el inglés en el juego.
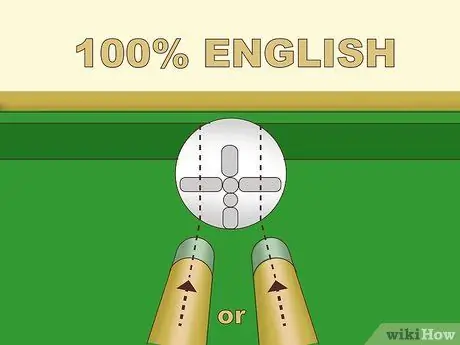
Paso 3. Practica varios puntos fuertes del inglés
Hay varios tipos de inglés, pero este artículo analiza solo las formas básicas. Si el palo se clavara a la izquierda del centro de la bola, la bola rotaría a lo largo de este eje; aquí está "English left". Cuando esta bola que gira golpea la superficie, el giro hará que la bola gire más hacia la izquierda que sin el inglés. Por el contrario, golpear a la derecha del centro de la bola blanca traerá "Inglés a la derecha" y rebotará la bola más a la derecha. Cuanto más empujes desde el centro de la pelota, mayor será el impacto:
- El inglés al 100% o máximo se hace pinchando el punto medio entre el centro y el borde de la pelota. Esta es la distancia máxima de empuje para obtener un empujón con un error mínimo.
- Inglés 50% se hace pinchando el punto medio entre el punto máximo y el centro de la pelota (¼ de la distancia entre el centro y el borde de la pelota).
- Puede utilizar porcentajes en inglés pinchando en varios puntos entre el centro y el punto máximo de la bola blanca.
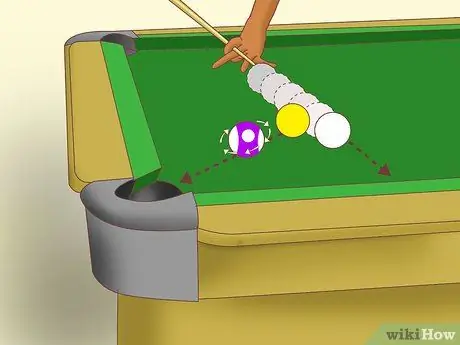
Paso 4. Comprender el engranaje
Cuando dos bolas chocan, la bola objeto comienza a girar sobre un eje determinado, de acuerdo con el ángulo del golpe y la cantidad de inglés ganado. Si puede lograr un "engranaje", esta rotación se produce a lo largo del eje de movimiento. En otras palabras, el movimiento de la bola objetivo no se ve afectado por la rotación. La pelota se deslizará a lo largo de la "línea central" o la línea trazada entre los centros de las dos bolas en el impacto.
El término proviene de la analogía de dos engranajes que funcionan sin problemas entre sí y transmiten el movimiento a la perfección
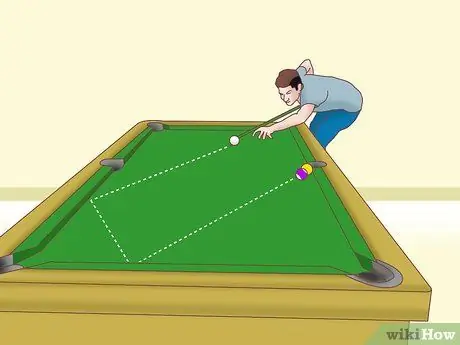
Paso 5. Ajuste el inglés para lograr un engranaje en todas las piezas
Una vez que haya lanzado una esquina usando el enfoque "completo" o "bola fantasma", es una buena idea asegurarse de que la bola objetivo no gire de manera extraña y arruine su tiro. Aquí hay una tabla que puede ayudarlo a encontrar el ángulo correcto y el inglés. Todos los números a continuación son "Inglés afuera", lo que significa que mueves el palo al lado de la bola blanca más allá de la bola objetivo.
- Si el ángulo de corte es de 15º, utilice un inglés ligeramente superior al 20%. (Recuerde, el ángulo de corte es el ángulo entre la trayectoria inicial de la bola blanca y la trayectoria de la bola del objeto).
- Si el ángulo de corte es de 30º, utilice el inglés al 40%.
- Si el ángulo de corte es de 45º, use 55% de inglés.
- Si el ángulo de corte es de 60º, use el inglés al 70%.
- Cuando el ángulo de corte se acerque a 90º, aumente el inglés al 80%.
Paso 6. Conozca el efecto del impacto sin engranajes
Si usa ingles menos de los muchos "engranajes" en el último paso, la bola blanca se desplazará hacia adelante durante el impacto, y el giro lateral se desplazará hacia la bola objetivo. Luego, la bola objeto se moverá ligeramente hacia la derecha desde el ángulo de corte estimado. Si su inglés es más que engranaje, la bola objetivo se moverá ligeramente hacia la izquierda del ángulo de corte estimado.
- Este efecto se denomina lanzamiento inducido por corte: el ángulo del corte desplaza el giro que hace que la pelota se desvíe ligeramente del rumbo.
- Puede utilizar esta técnica para realizar tomas que parecen casi imposibles. Si su único tiro es demasiado a la derecha, aumente su inglés para meter la bola en la tronera.
Consejos
- Si la bola objetivo está pegada al riel y necesita rodarla a lo largo del riel hacia la bolsa, siempre golpee el riel primero antes de tocar la bola objetivo. Por lo tanto, la bola blanca da impulso a la barandilla, en lugar de hacia ella. (Si el ángulo de impacto supera los 45º, deberá utilizar el inglés).
- Cuanto mayor sea el ángulo de impacto entre las dos bolas, menor será el impulso transmitido. Esto significa que tendrá que empujar un poco más fuerte para cortes delgados (grietas en ángulos extremos).
- Después del impacto, el ángulo entre la trayectoria de la bola blanca y la trayectoria de la bola del objeto debe ser siempre de 90º. Utilice este conocimiento para evitar que entren bolas blancas en la bolsa. Tenga en cuenta que el giro extremo puede romper esta regla y bolas de diferente masa (por ejemplo, en una mesa de billar común en un café).






