- Autor Jason Gerald [email protected].
- Public 2024-01-15 08:13.
- Última modificación 2025-01-23 12:16.
Dividir una fracción por una fracción puede parecer confuso al principio, pero en realidad es muy fácil. ¡Todo lo que tienes que hacer es voltear, multiplicar y simplificar! Este artículo lo guiará a través del proceso y le mostrará lo fácil que es dividir una fracción por una fracción.
Paso
Parte 1 de 2: Comprender cómo dividir fracciones por fracciones
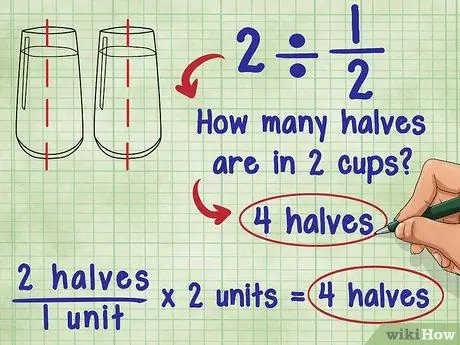
Paso 1. Piensa en lo que significa dividir por una fracción
Sobre 2 ÷ 1/2 preguntó Ada: "¿Cuántas mitades hay en 2?" La respuesta es 4 porque cada unidad (1) consta de dos "mitades", y hay 2 unidades en total: 2 "mitades" / 1 unidad * 2 unidades = 4 "mitades".
- Intente imaginar la misma ecuación usando un vaso de agua: ¿Cuántos vasos y medio de agua hay en 2 vasos de agua? Puede verter 2 tazas y media de agua en cada vaso de agua. Eso significa, básicamente, sumas los "medios" vasos de agua y tienes dos vasos: 2 "medio" / 1 taza * 2 tazas = 4 "medio".
- Esto significa que si la fracción que está dividiendo está entre 0 y 1, ¡la respuesta siempre es mayor que el número original! Esto es cierto cuando divide un número entero o una fracción por una fracción.

Paso 2. Comprende que dividir es lo opuesto a multiplicar
Por lo tanto, dividir por una fracción se puede resolver multiplicando por el recíproco de la fracción. El recíproco de una fracción (también llamado "multiplicación inversa") es la fracción que se invierte, de modo que el numerador y el denominador intercambian lugares. En un momento, dividiremos fracciones por fracciones, encontraremos el recíproco de la segunda fracción y multiplicaremos ambas fracciones. Sin embargo, veamos primero algunos de los opuestos:
- El recíproco de 3/4 es 4/3.
- Lo contrario de 7/5 es 5/7.
- El recíproco de 1/2 es 2/1 o 2.
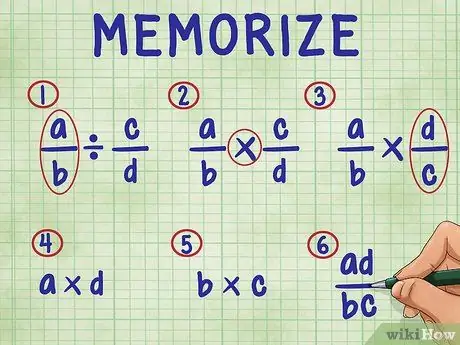
Paso 3. Recuerda los siguientes pasos para dividir una fracción por una fracción
En orden, los pasos incluyen:
- Solo deja la primera fracción en la ecuación.
- Cambia el signo de división por el signo de multiplicación.
- Invierte la segunda fracción (encuentra su recíproco).
- Multiplica el numerador (número superior) de ambas fracciones. El resultado de la multiplicación es el numerador (arriba) de su respuesta.
- Multiplica el denominador (número de abajo) de ambas fracciones. El producto del producto es el denominador de tu respuesta.
- Simplifica tus fracciones simplificándolas a sus términos más simples.
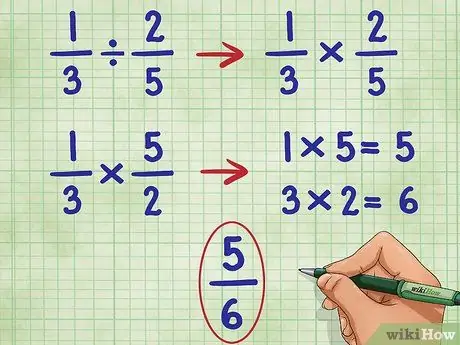
Paso 4. Realice estos pasos para el ejemplo 1/3 2/5
Comenzaremos omitiendo la primera fracción y convirtiendo el signo de división en el signo de multiplicación:
- 1/3 ÷ 2/5 = Se convierte en:
- 1/3 * _ =
- Ahora, invertimos la segunda fracción (2/5) para encontrar su recíproco, que es 5/2:
- 1/3 * 5/2 =
- Ahora, multiplique el numerador (número superior) de ambas fracciones, 1 * 5 = 5.
- 1/3 * 5/2 = 5/
- Ahora, multiplica el denominador (número de abajo) de ambas fracciones, 3 * 2 = 6.
- Ahora tenemos: 1/3 * 5/2 = 5/6
- Esta fracción no se puede simplificar más, por lo que tenemos nuestra respuesta.

Paso 5. Intenta recordar las siguientes rimas para ayudarte a recordar:
"Dividir fracciones es fácil, invierta la segunda fracción y luego multiplique. No olvide simplificar antes de que sea hora de comer".
Otro recordatorio útil le dice qué hacer con cada parte de la ecuación: "Déjame (primera fracción), Cambiarme (signo de división), Invertirme (segunda fracción)"
Parte 2 de 2: División de fracciones por fracciones en problemas
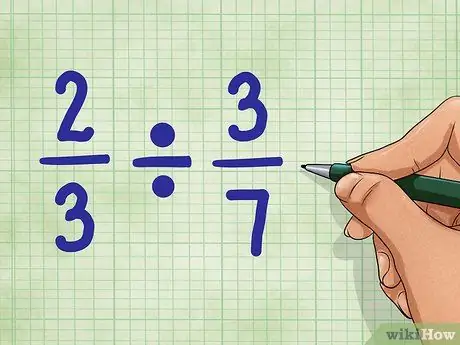
Paso 1. Empiece con preguntas de muestra
Usemos 2/3 ÷ 3/7. Esta pregunta solicita el número de partes igual a 3/7, que se puede encontrar en el valor 2/3. No te preocupes. ¡No es tan difícil como parece!
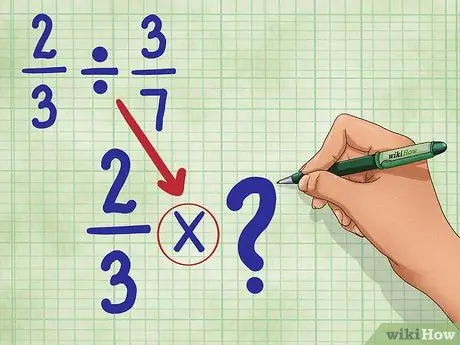
Paso 2. Convierta el signo de división en el signo de multiplicación
Tu nueva ecuación será: 2/3 * _ (Llenaremos este espacio en blanco en un momento).
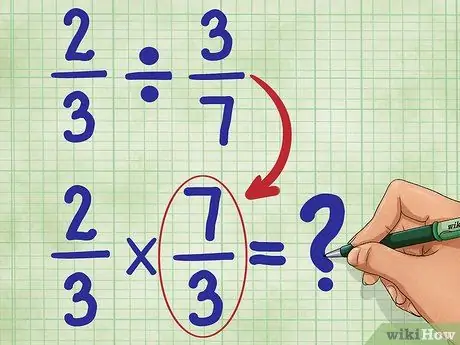
Paso 3. Ahora, encuentra el recíproco de la segunda fracción
Esto significa voltear 3/7 para que el numerador (3) esté ahora en la parte inferior y el denominador (7) esté ahora en la parte superior. El recíproco de 3/7 es 7/3. Ahora, escribe tu nueva ecuación:
2/3 * 7/3 = _

Paso 4. Multiplica tus fracciones
Primero, multiplica los numeradores de ambas fracciones: 2 * 7 = 14. 14 es el numerador (número superior) de su respuesta. Luego, multiplica los denominadores de ambas fracciones: 3 * 3 = 9. 9 es el denominador (número inferior) de su respuesta. Ahora sabes que 2/3 * 7/3 = 14/9.
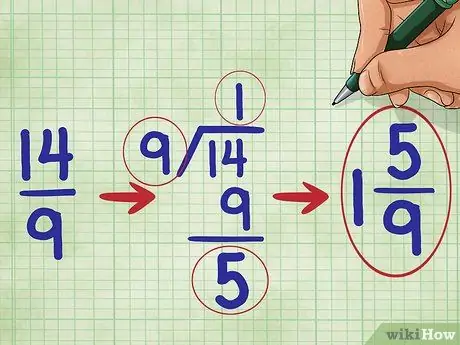
Paso 5. Simplifica tu fracción
En este problema, debido a que el numerador de la fracción es mayor que el denominador, sabemos que nuestra fracción es mayor que 1. Debemos convertirla en un número mixto. (Un número mixto es un número entero y una fracción combinados, por ejemplo, 1 2/3.))
-
Primero, divide el numerador
Paso 14. con 9.
El número 14 dividido por 9 es igual a uno con un resto de 5, por lo que debes escribir tu fracción simplificada como: 1 5/9 (“Uno cinco noveno”).
- ¡Detente, has encontrado la respuesta! Puede especificar que ya no puede simplificar la fracción porque el denominador no es divisible por el numerador (9 no es divisible por 5) y el numerador es un número primo o un entero que solo es divisible por uno y el número en sí.
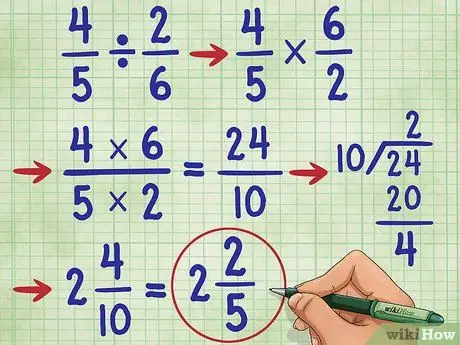
Paso 6. ¡Prueba con otro ejemplo
Probemos la pregunta 4/5 ÷ 2/6 =. Primero, cambie el signo de división por el signo de multiplicación (4/5 * _ =), luego encuentre el recíproco de 2/6, que es 6/2. Ahora tienes la ecuación: 4/5 * 6/2 =_. Ahora, multiplique el numerador, 4 * 6 = 24, y el denominador 5* 2 = 10. Ahora tu tienes 4/5 * 6/2 = 24/10.
Ahora, simplifica la fracción. Dado que el numerador es mayor que el denominador, debemos convertir esta fracción en un número mixto.
- Primero, divida el numerador por el denominador, (24/10 = 2 restantes 4).
- Escribe la respuesta como 2 4/10. ¡Todavía podemos simplificar esta fracción nuevamente!
- Tenga en cuenta que 4 y 10 son números pares. Entonces, el primer paso para simplificarlo es dividir cada número por 2. Obtenemos 2/5.
- Dado que el denominador (5) no es divisible por el numerador (2) y 5 es un número primo, sabemos que esta fracción no se puede simplificar más. Entonces, nuestra respuesta es: 2 2/5.

Paso 7. Obtén ayuda adicional para simplificar fracciones
Probablemente dedicaste mucho tiempo a aprender a simplificar fracciones antes de intentar dividirlas entre sí. Sin embargo, si necesita un repaso o alguna otra ayuda, hay algunos artículos en línea excelentes que pueden ser de gran ayuda para usted.
Artículos relacionados de wikiHow
- Convertir fracciones comunes a decimales
- Calcular el área de un círculo
- División de polinomios mediante división sintética
- División de fracciones mixtas






