En estadística, el rango es la diferencia entre el valor más alto de un conjunto de datos y el valor más bajo de un conjunto de datos. El rango muestra qué tan dispersos están los valores en una serie. Si el rango es un número grande, los valores de la serie están muy dispersos; si el rango es un número pequeño, los valores de la serie están próximos entre sí. Si desea saber cómo calcular el alcance, simplemente siga estos pasos.
Paso
Paso 1. Enumere los elementos de su conjunto de datos
Para encontrar el rango de un conjunto de datos, debe enumerar todos los elementos del conjunto de datos para poder identificar los números más grandes y más pequeños. Anote todos los elementos. Los números en este conjunto de datos son: 14, 19, 20, 24, 25 y 28.
- Es más fácil identificar los números más grandes y más pequeños en un conjunto de datos si ordena los números de menor a mayor. En este ejemplo, el conjunto de datos se estructuraría así: 14, 19, 20, 24, 24, 25, 28.
- Ordenar los elementos de un conjunto de datos también le ayudará a realizar otros cálculos, como encontrar la moda, la media o la mediana del conjunto de datos.
Paso 2. Identifique los números más grandes y más pequeños del conjunto de datos
En este problema, el número más pequeño del conjunto de datos es 14 y el número más grande es 28.
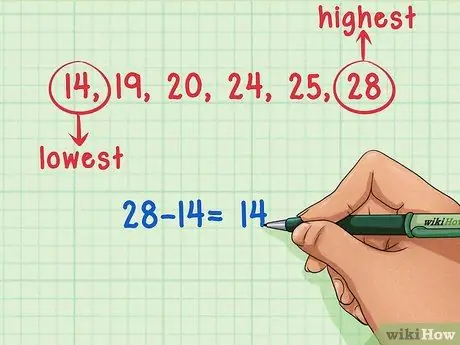
Paso 3. Reste el número más pequeño en su conjunto de datos del número más grande
Ahora que ha identificado los números más pequeños y más grandes en el conjunto de datos, todo lo que tiene que hacer es restarlos entre sí. Reste 14 de 25 (25 - 14) para obtener 11, el rango del conjunto de datos.
Paso 4. Rotule el rango claramente
Una vez que encuentre el rango, etiquételo claramente. Esto le ayudará a evitar confusiones con otros cálculos estadísticos que pueda tener que realizar, como encontrar la mediana, la moda o la media.
Consejos
- También puede interpretar el rango en términos algebraicos, pero primero debe comprender el concepto de una función algebraica o un conjunto de operaciones con números conocidos. Debido a que las operaciones de función se pueden realizar en cualquier número, incluso un número desconocido, el número se denota mediante una letra variable, generalmente x. Un dominio es un conjunto de posibles valores de entrada, que puede sustituir por el número desconocido. Por lo tanto, el rango es el conjunto de posibles resultados de cálculo, que obtiene después de ingresar uno de los valores de dominio y completar todas las operaciones definidas por la función. Desafortunadamente, no hay forma de calcular el rango de una función. A veces, graficar una función o calcular varios valores puede mostrar un patrón claro. También puede utilizar su conocimiento del dominio de la función para descartar posibles valores de salida (resultados de cálculo) o reducir el conjunto de datos que representa el rango.
- El valor mediano de cualquier conjunto de datos estadísticos representa el valor mediano del conjunto de datos en términos de distribución de datos, no rango. Entonces, si bien es posible que desee suponer que la mediana de un conjunto de datos dado es el rango dividido por 2, o la mitad del rango del rango, esto generalmente no es cierto. Para encontrar la mediana correcta, debe ordenar los elementos de datos y luego buscar el elemento en el medio de la lista. Este elemento es la mediana. Por ejemplo, si tiene una lista de 29 elementos, el decimoquinto elemento tiene el mismo rango desde el principio y el final de la lista, por lo que el decimoquinto elemento es la mediana, independientemente de cómo se relacione el valor de ese elemento con el rango.
