IQR es el rango intercuartil o el rango de la raíz del cuartil de un conjunto de datos. IQR se utiliza en análisis estadístico para ayudar a sacar conclusiones sobre un conjunto de datos. IQR se usa con más frecuencia que el rango porque IQR no incluye los datos más externos. ¡Continúe leyendo para aprender cómo encontrar el IQR!
Paso
Método 1 de 3: Comprensión de IQR
Paso 1. Comprenda cómo usar IQR
Básicamente, IQR es una forma de entender la distribución de un conjunto de números. El rango del cuartil raíz se define como la diferencia entre el cuartil superior (25% superior) y el cuartil inferior (25% inferior) del conjunto de datos.
Propina:
El cuartil inferior generalmente se escribe como Q1, y el cuartil superior se escribe como Q3, lo que técnicamente hace que el punto medio de los datos sea Q2 y el punto más alto como Q4.
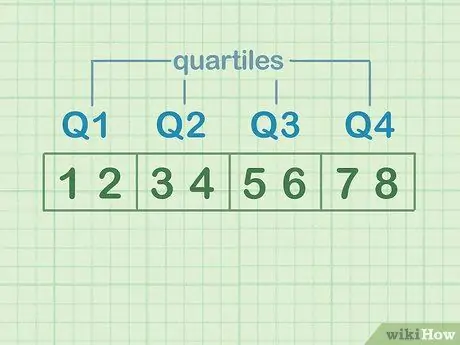
Paso 2. Comprende los cuartiles
Para ilustrar los cuartiles, divida el conjunto de números en cuatro partes iguales. Cada una de estas partes es un "cuartil". Suponga que los conjuntos de datos son: 1, 2, 3, 4, 5, 6, 7, 8.
- 1 y 2 son el primer cuartil o Q1
- 3 y 4 son el segundo cuartil o Q2
- 5 y 6 son el tercer cuartil o Q3
- 7 y 8 son el cuarto cuartil o Q4
Paso 3. Aprenda la fórmula
Para encontrar la diferencia entre los cuartiles superior e inferior, debe restar el percentil 75 del percentil 25.
La fórmula está escrita: Q3 - Q1 = IQR
Método 2 de 3: compilación del conjunto de datos
Paso 1. Recopile sus datos
Si estudia IQR en clase y en exámenes, es posible que le den un conjunto de datos ya preparados, por ejemplo 1, 4, 5, 7, 10. Este es su conjunto de datos: los números con los que trabajará. Sin embargo, puede construir sus propios números a partir de preguntas de mesa o problemas de historias.
Asegúrese de que cada número represente lo mismo:
por ejemplo, el número de huevos en cada nido de una población de aves definida, o el número de espacios de estacionamiento ubicados en cada casa en un bloque específico.
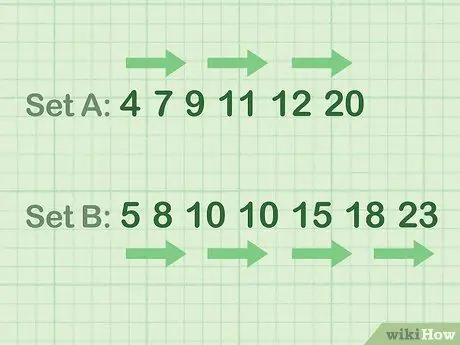
Paso 2. Ordene sus datos en orden ascendente
En otras palabras: organice los números de menor a mayor. Utilice las sugerencias de los siguientes ejemplos.
- Ejemplo de datos de números pares (conjunto A): 4 7 9 11 12 20
- Ejemplo de datos de números impares (Conjunto B): 5 8 10 10 15 18 23
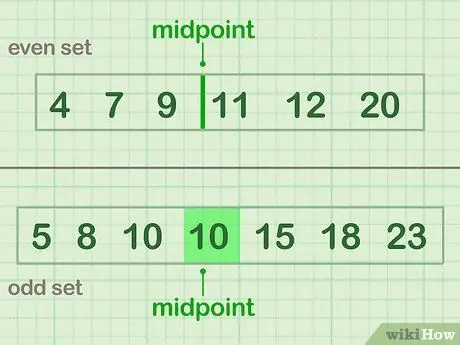
Paso 3. Divida los datos en dos
Para dividir por la mitad, encuentre el punto medio de sus datos: el número o números que están en el centro del conjunto de datos. Si tiene un número impar de datos, elija el número que está justo en el medio. Si tiene un número par de datos, el punto medio se encuentra entre los dos números más intermedios.
- Un ejemplo par (conjunto A) que tiene un punto medio entre 9 y 11: 4 7 9 | 11 12 20
- Un ejemplo extraño (conjunto B) que tiene un punto medio de valor (10): 5 8 10 (10) 15 18 23
Método 3 de 3: Calcular IQR
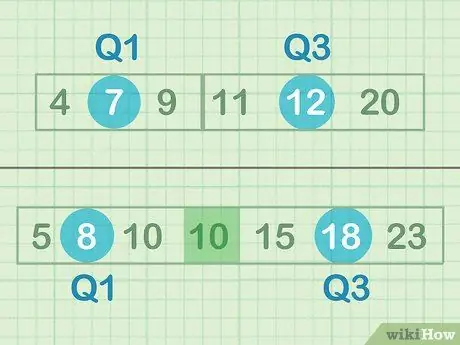
Paso 1. Encuentre la mediana de su mitad inferior y superior de los datos
La mediana es el "punto medio" o número que está en el medio de un conjunto de números. En este caso, no busca el punto medio de todos los números, sino el punto medio relativo de los subconjuntos de datos superior e inferior. Si tiene un número impar de datos, no incluya el número del medio; por ejemplo, en el conjunto B, no es necesario que incluya un solo 10.
-
Incluso ejemplo (conjunto A):
- Mediana de la mitad inferior de los datos = 7 (Q1)
- Mediana de la mitad superior de los datos = 12 (Q3)
-
Ejemplo extraño (conjunto B):
- Mediana de la mitad inferior de los datos = 8 (Q1)
- Mediana de la mitad superior de los datos = 18 (Q3)
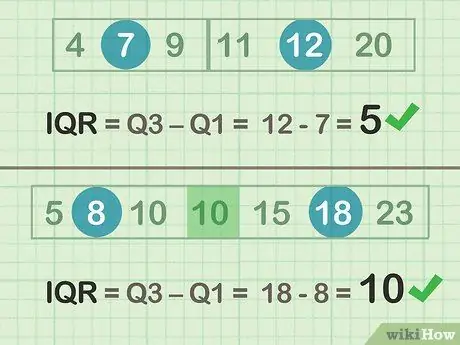
Paso 2. Reste Q3-Q1 para determinar el IQR
Ahora ya sabe cuántos números se encuentran entre los percentiles 25 y 75. Puede utilizar este número para comprender la distribución de datos. Por ejemplo, si una prueba tiene una puntuación máxima de 100 y el IQR de la puntuación es 5, puede suponer que la mayoría de las personas que realizan la prueba tienen casi la misma comprensión porque el rango de altibajos no es muy grande. Sin embargo, si el IQR de la puntuación de una prueba es 30, es posible que empiece a preguntarse por qué algunas personas obtienen una puntuación tan alta y otras tan bajas.
- Ejemplo par (conjunto A): 12-7 = 5
- Ejemplo extraño (conjunto B): 18 - 8 = 10
Consejos
Es importante aprender a hacer esto por su cuenta. Sin embargo, hay varias calculadoras de IQR en línea que puede usar para verificar su trabajo. ¡No confíe demasiado en las aplicaciones de calculadora si aprende esto en clase! Si se le pide que busque el IQR en una prueba, deberá saber cómo encontrarlo manualmente
WikiHow relacionado
- Cómo detectar valores atípicos
- Cómo calcular el rango de un conjunto de datos
- Cómo hacer un diagrama de caja y tienda
