- Autor Jason Gerald [email protected].
- Public 2023-12-16 11:06.
- Última modificación 2025-01-23 12:16.
Para la mayoría de las personas, las fracciones son los primeros cálculos complicados que se encuentran. El concepto de fracciones es bastante difícil y requiere que aprendas condiciones especiales para hacerlo. Debido a que las fracciones tienen reglas especiales para sumar, restar, multiplicar y dividir, muchas personas están confundidas al respecto. Sin embargo, con mucha práctica, cualquiera puede aprender y completar cálculos relacionados con fracciones.
Paso
Método 1 de 5: Entender las fracciones
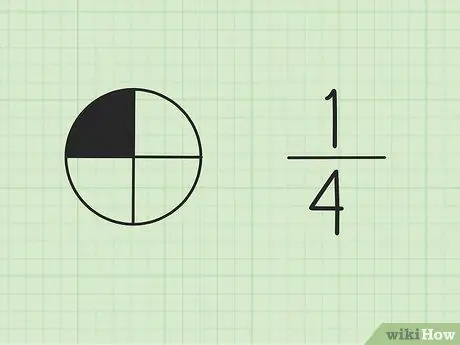
Paso 1. Comprende que las fracciones son parte de un todo
El número en la parte superior se llama numerador y representa el número de partes del total. El número en la parte inferior se llama denominador, que representa el número total de partes.
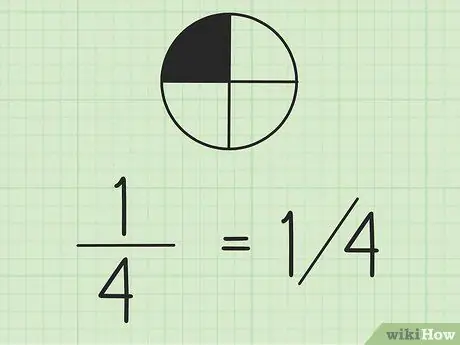
Paso 2. Tenga en cuenta que puede escribir fracciones con barras
El número de la izquierda es el numerador y el número de la derecha es el denominador. Si está trabajando con fracciones en la misma línea, es una buena idea escribir el numerador sobre el denominador.
Por ejemplo, si toma una de las cuatro porciones de pizza, tiene pizza. Si tiene 7/3 pizzas, eso significa que tiene dos pizzas enteras más 1 de 3 porciones de pizza
Método 2 de 5: diferencia entre fracciones simples y mixtas

Paso 1. Comprender que los números mixtos consisten en números enteros y fracciones, por ejemplo, 2 1/3 o 45 1/2
Por lo general, debe convertir números mixtos a una forma más simple para sumar, restar, multiplicar o dividir.

Paso 2. Cambie el número mixto multiplicando el número entero por el denominador de la fracción y luego sumándolo por el numerador
Escribe el resultado como numerador, mientras que el denominador no cambia.
Por ejemplo, para convertir 2 1/3 en una fracción simple, multiplica 2 por 3, luego suma 1 y obtén 7/3

Paso 3. Convierta fracciones simples en números mixtos dividiendo el numerador por el denominador
El resultado total de la división se escribe como un número entero y el resto de la división se escribe como el numerador de la fracción. El denominador no cambia.
Por ejemplo, para convertir 7/3 en un número mixto, divida 7 entre 3 para obtener 2 con un resto de 1. Entonces, el número mixto es 2 1/3. Las fracciones simples solo se pueden convertir en números mixtos si el numerador es mayor que el denominador
Método 3 de 5: sumar y restar fracciones
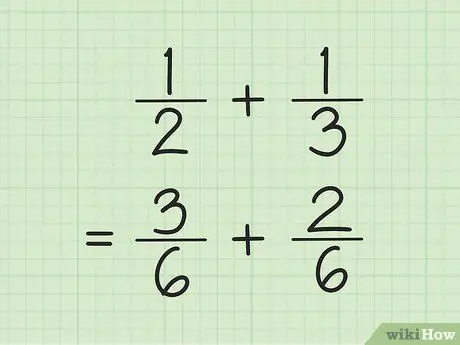
Paso 1. Encuentra un denominador común para sumar y restar fracciones
El truco, multiplica los números en el denominador, luego multiplica cada numerador por el número utilizado para encontrar el denominador. A veces, puedes encontrar el MCM (mínimo común múltiplo) para el denominador multiplicando los denominadores entre sí.
Por ejemplo, para sumar y 1/3, primero encuentre el MCM (mínimo común múltiplo) de los dos denominadores multiplicándose entre sí. Por lo tanto, multiplica 2 y 3 para obtener el MCM 6. Multiplica 1 por 3 para obtener 3 como el nuevo numerador de la primera fracción. Multiplica 1 por 2 para obtener 2 como el nuevo numerador de la segunda fracción. Tus nuevas fracciones son 3/6 y 2/6
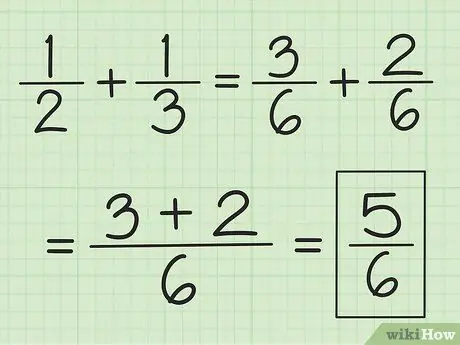
Paso 2. Suma los dos numeradores y no cambies el denominador
Por ejemplo, 3/6 más 2/6 es 5/6 y 2/6 más 1/6 es 3/6
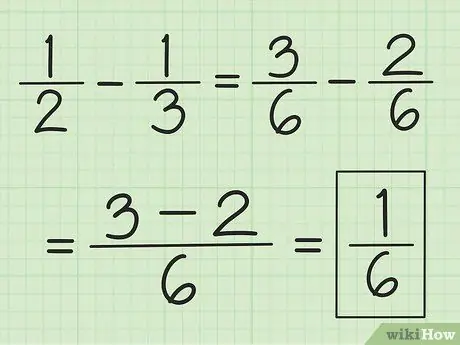
Paso 3. Usa una técnica similar para restar
Encuentre primero el MCM de los denominadores, pero en lugar de sumarlos, reste el número del primer numerador por el número del segundo.
Por ejemplo, para restar 1/3 de 1/2, primero cambie las fracciones a 3/6 y 2/6, luego reste 3 por 2 para obtener 1. Esto da como resultado 1/6
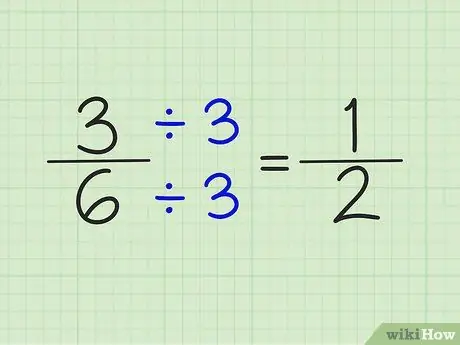
Paso 4. Simplifique las fracciones dividiendo el numerador y el denominador por el mismo número
Por ejemplo, el número 5/6 no se puede simplificar. Sin embargo, 3/6 se puede simplificar dividiendo el numerador y el denominador por el número 3. El resultado es una fracción de 1/2

Paso 5. Convierta la fracción en un número mixto si el numerador es mayor que el denominador
Método 4 de 5: multiplica y divide fracciones
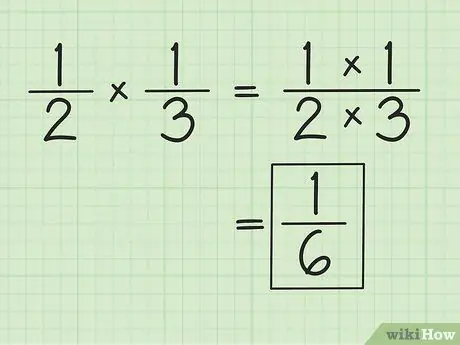
Paso 1. Multiplica el numerador y el denominador por separado para multiplicar fracciones
Por ejemplo, al multiplicar por 1/3, el resultado es 1/6 (1 por 1 y 2 por 3). No es necesario que coincida con los denominadores al multiplicar fracciones. Simplifique o modifique los resultados obtenidos, si es necesario
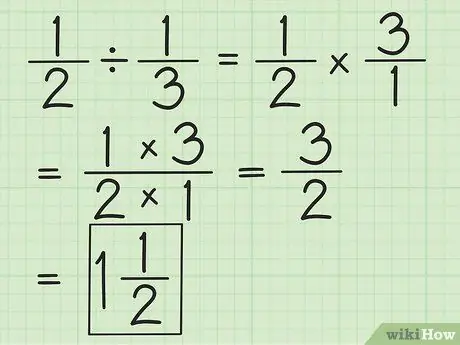
Paso 2. Divide dos fracciones invirtiendo la segunda fracción y luego multiplicando ambas
Por ejemplo, si desea dividir 1/2 entre 1/3, primero invierta la segunda fracción a 3/1. Multiplica por 3/1 y obtén 3/2. Simplifique fracciones o conviértalas a números mixtos, si es posible
Método 5 de 5: Trabajar con fracciones complejas
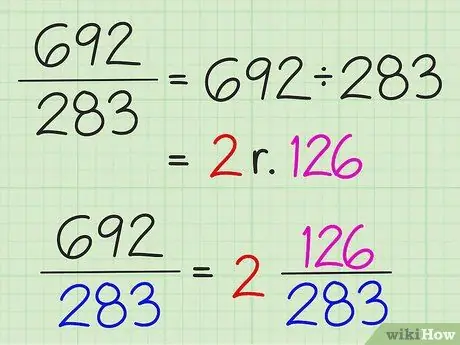
Paso 1. Trabaja todas las fracciones de la misma manera, incluso si el problema parece muy complicado
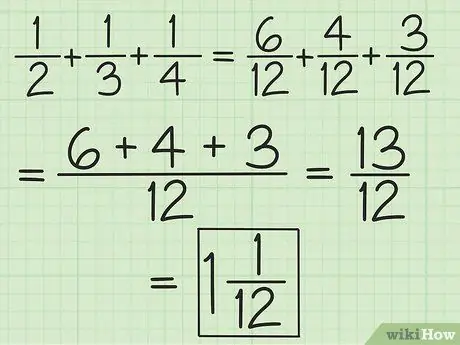
Paso 2. Empareja los denominadores de todas las fracciones o trabaja en pares comenzando de izquierda a derecha para sumar y restar más de dos fracciones
Por ejemplo, para sumar 1/2, 1/3 y 1/4, puede cambiarlos a 6/12, 4/12 y 3/12 para obtener 13/12, o puede agregar 3/6 y 2 / 6 para obtener 5/6, luego agregue 5/6 y 1/4 (iguale los denominadores para que la segunda fracción se convierta en 3/12) para obtener 13/12 (10/12 más 3/12). Conviértelo en un número mixto, que es 1 1/12
Consejos
- Recuerda que has aprendido bastante matemáticas. Las matemáticas son como un idioma que puedes pronunciar con fluidez y ahora estás tratando de aprender a leerlo y escribirlo.
- Recuerde siempre simplificar el resultado final de su cálculo, ya sea que su problema tenga la forma de una fracción ordinaria, un número mixto o una fracción compleja.






