- Autor Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-19 22:12.
- Última modificación 2025-01-23 12:16.
Las matemáticas son difíciles. Es fácil olvidar incluso los conceptos básicos cuando intenta recordar los diferentes principios y métodos. Aquí hay dos formas nuevas de simplificar fracciones.
Paso
Método 1 de 4: uso del máximo factor común

Paso 1. Escribe los factores del numerador y del denominador
Los factores son números que puedes multiplicar para obtener otro número. Por ejemplo, 3 y 4 son factores de 12 porque puedes multiplicarlos para obtener 12. Para escribir los factores de un número, solo necesitas escribir todos los números que se pueden multiplicar para obtener ese número, y son divisibles. por los factores.
-
Escribe los factores del número de menor a mayor, sin olvidar incluir el factor 1. Por ejemplo, así es como escribes el numerador y el denominador de la fracción 24/32:
- 24: 1, 2, 3, 4, 6, 8, 12, 24.
- 32: 1, 2, 4, 8, 16, 32.

Paso 2. Encuentra el máximo factor común (MCD) del numerador y denominador
GCF es el número más grande que puede dividir uniformemente dos o más números. Después de haber anotado todos los factores del número, todo lo que tiene que hacer es encontrar el número más grande que sea el mismo en ambas listas de factores.
-
24: 1, 2, 3, 4, 6,
Paso 8., 12, 24.
-
32: 1, 2, 4,
Paso 8., 16, 32.
-
El MCD de 24 y 32 es 8 porque 8 es el número más grande que puede dividir uniformemente 24 y 32.

Paso 3. Divida el numerador y la fracción por el MCD
Ahora que tienes el MCD, todo lo que tienes que hacer es dividir el numerador y el denominador por ese número para simplificar tu fracción a su forma más simple. He aquí cómo hacerlo:
- 24/8 = 3
- 32/8 = 4
- La fracción simple es 3/4.

Paso 4. Revise su trabajo
Si desea asegurarse de haber simplificado la fracción correctamente, solo necesita multiplicar el nuevo numerador y denominador por su MCD para recuperar la fracción original. He aquí cómo hacerlo:
- 3 * 8 = 24
- 4 * 8 = 32
-
Ha vuelto a su forma original, que es 24/32.
También puede verificar la fracción para asegurarse de que no se pueda simplificar más. Dado que 3 es un número primo, solo se puede dividir entre 1 y él mismo, y cuatro no es divisible entre 3, por lo que la fracción no se puede simplificar más
Método 2 de 4: sigue dividiendo por números pequeños

Paso 1. Elija un número pequeño
Con este método, solo tiene que elegir un número pequeño, como 2, 3, 4, 5 o 7, para empezar. Mira las fracciones para asegurarte de que cada parte sea divisible por el número que elegiste. Por ejemplo, si tiene una fracción 24/108, no elija 5 porque no son divisibles entre 5. Sin embargo, si tiene una fracción 25/60, 5 es el número correcto para usar.
Para la fracción 24/32, 2 es un buen número. Dado que ambos números son pares, son divisibles por 2

Paso 2. Divide el numerador y el denominador de la fracción por el número
La nueva fracción constará de un nuevo numerador y denominador, que se obtiene después de dividir la parte superior e inferior de la fracción 24/32 entre 2. A continuación, le indicamos cómo hacerlo:
- 24/2 = 12
- 32/2 = 16
- Tu nueva fracción es 12/16.
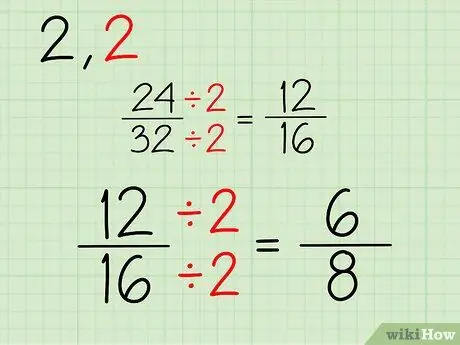
Paso 3. Repita
Continúe este proceso. Como ambos números son pares, puedes seguir dividiendo por 2. Si uno o ambos numeradores y denominadores son números impares, puedes intentar dividir por otro número. Este es el proceso para simplificar la fracción 12/16:
- 12/2 = 6
- 16/2 = 8
- Tu nueva fracción es 6/8.

Paso 4. Sigue dividiendo el número hasta que ya no sea divisible
El nuevo numerador y denominador también son números pares, por lo que puede seguir dividiendo por 2. A continuación, le indicamos cómo hacerlo:
- 6/2 = 3
- 8/2 = 4
- Tu nueva fracción es 3/4.

Paso 5. Asegúrese de que la fracción no se pueda simplificar más
En la fracción 3/4, 3 es un número primo, por lo que los factores son solo 1 y él mismo, y 4 no es divisible por 3, por lo que la fracción no se puede simplificar más. Si el numerador o denominador de la fracción ya no se puede dividir por el número que seleccionó, es posible que aún pueda dividirlo por otro número.
Por ejemplo, si tiene la fracción 10/40 y divide el numerador y el denominador entre 5, el resultado es 2/8. No puede seguir dividiendo el numerador y la fracción por 5, pero puede dividir ambos por 2 para que el resultado final sea 1/4

Paso 6. Revise su trabajo
Multiplica 3/4 por 2/2 nuevamente tres veces, para asegurarte de obtener la fracción inicial, que es 24/32. He aquí cómo hacerlo:
- 3/4 * 2/2 = 6/8
- 6/8 * 2/2 = 12/16
- 12/16 * 2/2 = 24/32.
- Observe que está dividiendo 24/32 por 2 * 2 * 2, que es lo mismo que dividir por 8, el MCD más grande de 24 y 32.
Método 3 de 4: escribir los factores

Paso 1. Escribe tu fracción
Deje un espacio grande en el lado derecho de su papel; lo necesitará para anotar los factores.

Paso 2. Escribe los factores del numerador y el denominador
Solo los factores de los dos. La forma más sencilla es que los factores se escriban uno encima del otro. Empiece con el número 1 y anote los factores.
-
Por ejemplo, si su fracción es 24/60, comience con 24.
Anote: 24 - 1, 2, 3, 4, 6, 8, 12, 24
-
Luego, el número 60.
Anote: 60 - 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60

Paso 3. Encuentra y divide por el máximo factor común
Este término puede escribirse como GCF en su libro impreso. ¿Cuál es el número más grande que puede dividir el numerador y el denominador? Cualquiera que sea el número, divida ambos números por ese número.
Para nuestro ejemplo, el número más grande que es un factor de ambos números es 12. Por lo tanto, dividimos 24 entre 12 y 60 entre 12, lo que nos da 2/5, ¡nuestra fracción simple
Método 4 de 4: Uso de un árbol de factores primos

Paso 1. Encuentra los factores primos del numerador y denominador
Un número primo es un número que no se puede dividir por ningún otro número (que no sea él mismo y 1, por supuesto). 2, 3, 5, 7 y 11 son ejemplos de números primos.
- Empiece por el numerador. De 24, divídalo en 2 y 12. Dado que 2 ya es un número primo, ¡ya no necesita dividirlo! Luego, divide 12 en 2 números: 2 y 6. 2 son números primos, ¡genial! Ahora divida 6 en 2 números: 2 y 3. Ahora tiene 2, 2, 2 y 3 como números primos.
- Ahora trabaja en el denominador. A partir de 60, divide tu árbol en 2 y 30. 30 y luego divide en 2 y 15. Luego divide 15 en 3 y 5, los cuales son números primos. Ahora tienes 2, 2, 3 y 5 como números primos.
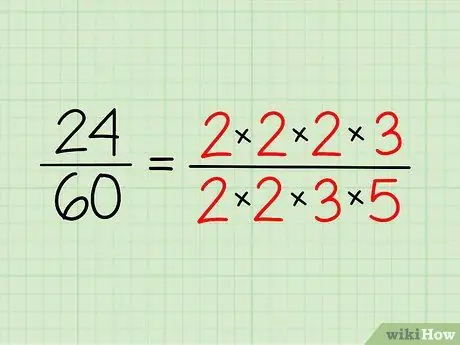
Paso 2. Escribe la factorización prima de cada número
Escribe los números primos que tienes para cada número y escríbelos en forma de multiplicación. No tiene que multiplicarlo, es solo una forma de hacer que sea más fácil de ver.
- Entonces, para 24, tienes 2 x 2 x 2 x 3 = 24.
- Para 60, tienes 2 x 2 x 3 x 5 = 60

Paso 3. Elimina los mismos factores
Cualquier número que forme parte de ambos números puede descartarse. En este ejemplo, los factores iguales son un par de 2 y un 3. ¡Adiós!
- El resto son 2 y 5, ¡o 2/5! La misma respuesta que obtuvimos en el camino anterior.
- Si el numerador y el denominador de la fracción son números pares, no se limite a dividir entre dos. Continúe haciendo la división hasta que el número que obtenga no pueda dividirse nuevamente.






