- Autor Jason Gerald [email protected].
- Public 2024-01-15 08:13.
- Última modificación 2025-01-23 12:16.
Hay varias formas de realizar la división. Puede dividir decimales, fracciones o incluso exponentes y usar una división larga o corta. Si desea conocer las diferentes formas de dividir números, siga los pasos a continuación.
Paso
Método 1 de 5: Realización de la división de series largas

Paso 1. Escriba las preguntas
Para hacer una división larga, coloque el denominador (el número que se dividirá) fuera de la barra divisoria y el numerador (el número que se dividirá) dentro de la barra divisoria.
Por ejemplo: 136 ÷ 3

Paso 2. Divida el primer dígito del numerador por el denominador (si es posible)
En este ejemplo, 1 no es divisible por 3, así que coloque un 0 encima de la barra divisoria y continúe con el siguiente paso. Reste 1 por 0 y coloque el resultado debajo del número 1.

Paso 3. Divida el número del resto del primer dígito del numerador y el segundo dígito del numerador por el denominador
Dado que 1 no se puede dividir entre 3, se sigue utilizando el número 1. Necesitas restar 3. Ahora, divide 13 entre 3. Dado que 3 x 4 = 12, coloca el 4 encima de la barra divisoria (a la derecha de 0), luego resta 13 entre 12 y escribe el resultado debajo.

Paso 4. Divide los números restantes por el denominador
Baje el número 6 a la derecha del 1 para obtener 16. Ahora, divida 16 entre 3. Como 3 x 5 = 15, escriba el número 5 a la derecha del número 4, reste 16 entre 15 y escriba el resultado (16-15 = 1) debajo.

Paso 5. Escribe el resto junto al cociente
Su respuesta final es 45 con 1 restante, o 45 R1.
Método 2 de 5: Realización de divisiones cortas

Paso 1. Escriba las preguntas
Escribe el denominador (el número a dividir) fuera de la barra divisoria y el numerador (el número a dividir) dentro de la barra divisoria. Tenga en cuenta que en la división corta, el denominador no puede tener más de un dígito.
Por ejemplo, 518 4

Paso 2. Divida el primer dígito del numerador por el denominador
5 4 = 1 R1. Coloque el cociente (1) sobre la barra divisoria larga. Escribe el resto sobre el primer dígito del numerador. Coloque un pequeño 1 sobre 5 para recordarle que le queda 1 cuando divide 5 entre 4. El 518 ahora debería verse así: 5118

Paso 3. Divida el número formado por el resto y el segundo dígito del numerador por el denominador
El siguiente número es 11 que se obtiene del valor residual (1) y el segundo dígito del numerador (1). 11 4 = 2 R 3 porque 4 x 2 = 8 con un resto de 3. Escribe el valor residual sobre el segundo dígito del numerador. Ponga 3 sobre 1. El numerador inicial (518) ahora se ve así: 51138

Paso 4. Divide los números restantes por el denominador
El número restante es 38; el número 3 proviene del resto de la etapa anterior y el 8 es el último dígito del numerador. Calcula 38 4 = 9 R2. Dado que 4 x 9 = 36, escriba "R2" encima de la barra de división porque 38 - 36 = 2.

Paso 5. Escriba la respuesta final
El resultado final y el cociente están por encima de la barra divisoria. La respuesta es 518 4 = 129 R2.
Método 3 de 5: dividir fracciones

Paso 1. Escriba las preguntas
Para dividir una fracción, simplemente escriba la primera fracción seguida del símbolo de división y luego la segunda fracción.
Por ejemplo: 3/4 5/8

Paso 2. Invierte el numerador y el denominador de la segunda fracción
La segunda fracción ahora es recíproca.
Ejemplo: 3/4 8/5

Paso 3. Cambie el símbolo de división por el símbolo de tiempos
Para dividir una fracción, multiplica la primera fracción por el recíproco de la segunda.
Ejemplo: 3/4 x 8/5
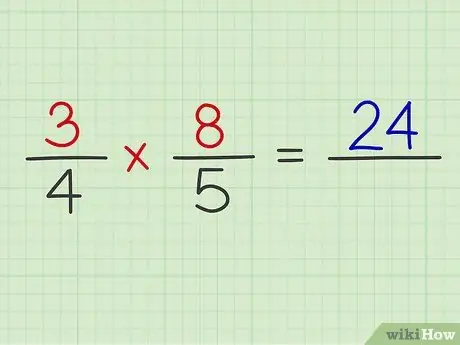
Paso 4. Multiplica el numerador de ambas fracciones
Simplemente hazlo como multiplicar dos fracciones regulares.
Ejemplo: 3 x 8 = 24
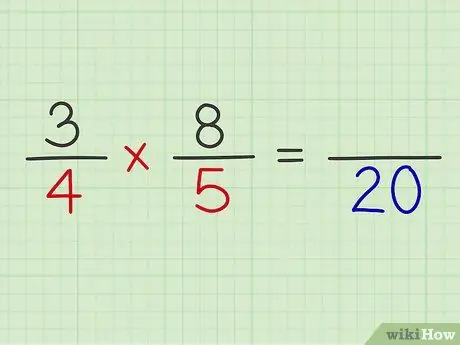
Paso 5. Multiplica los denominadores de ambas fracciones
Completa el cálculo multiplicando las dos fracciones.
Ejemplo: 4 x 5 = 20
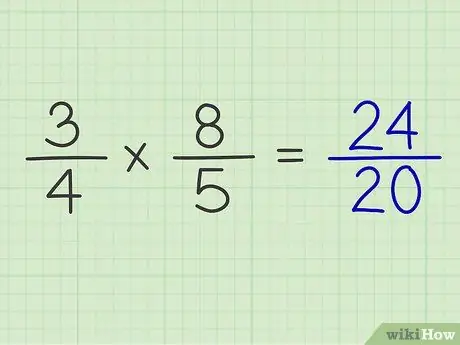
Paso 6. Coloque el producto del numerador sobre el producto del denominador
Después de multiplicar el numerador y el denominador de las dos fracciones, puedes obtener el resultado de calcular ambas fracciones.
Ejemplo: 3/4 x 8/5 = 24/20

Paso 7. Simplifica fracciones
Para encontrar el máximo común divisor, o el número más grande que divide el numerador y el denominador por igual. En este caso, el máximo común divisor de 24 y 20 es 4. Para demostrarlo, escribe todos los numeradores y denominadores y encierra en un círculo el número de los mayores factores comunes de ambos.
- 24: 1, 2, 3, 4, 6, 8, 12, 24
-
20: 1, 2, 4, 5, 10, 20
- Dado que 4 es el máximo común divisor de 24 y 20, simplemente divide los dos números entre 4 para simplificar la fracción.
- 24/4 = 6
- 20/4 = 5
- 24/20 = 6/5

Paso 8. Reescribe la fracción como un número mixto (opcional)
El truco, simplemente divide el numerador por el denominador y escribe el resultado como un número entero. Después de eso, escribe el resto de la división como un nuevo numerador y el denominador de la fracción no cambia. Dado que 6 dividido por 5 da como resultado 1 con un resto de 1, escriba el número entero 1, seguido del nuevo numerador 1, luego el denominador 5 para obtener un número mixto 1 1/5.
Ejemplo: 6/5 = 1 1/5
Método 4 de 5: Dividir exponente

Paso 1. Asegúrate de que los exponentes / potencias tengan el mismo número base
Solo puedes dividir exponentes si tienen el mismo número base. De lo contrario, puede intentar manipularlos hasta obtener el mismo número base.
Ejemplo: x8 X5

Paso 2. Resta el exponente
Simplemente puede restar el primer exponente por el segundo. No te preocupes por los números base por ahora.
Ejemplo: 8 - 5 = 3
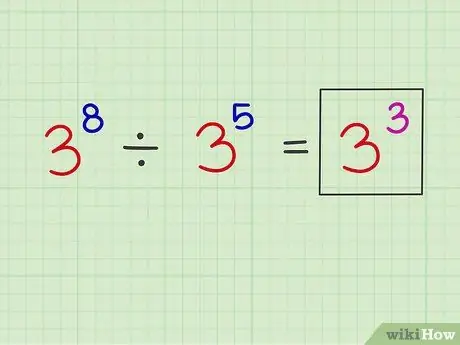
Paso 3. Coloque el nuevo exponente sobre el número base original
Ahora, puede escribir el nuevo exponente sobre el número base original.
Ejemplo: x8 X5 = x3
Método 5 de 5: División de números decimales

Paso 1. Escriba las preguntas
Escribe el denominador (el número a dividir) fuera de la barra divisoria y el numerador (el número a dividir) dentro de la barra divisoria. En la división decimal, su objetivo es convertir un número decimal en un número entero.
Ejemplo: 65.5.5

Paso 2. Cambia el denominador a un número entero
Simplemente deslice el punto decimal un dígito hacia la derecha para cambiar de 0,5 a 5, también conocido como 5, 0.

Paso 3. Cambie el numerador desplazando el punto decimal el mismo número de dígitos que el denominador
Debido a que mueve el punto decimal del numerador un dígito a la derecha para que se convierta en un número entero, el punto decimal del denominador también se desplaza un dígito a la derecha para que 65.5 cambie a 655.
Si desplaza el punto decimal del numerador más allá de todos sus dígitos, significa que debe agregar ceros a los dígitos cada vez que se desplaza el punto decimal. Por ejemplo, si el punto decimal 7, 2 se desplaza tres dígitos a la derecha, el número cambia a 7.200 porque el espacio en blanco de dos dígitos está lleno de ceros

Paso 4. Coloque el punto decimal en la barra de división larga justo encima del punto decimal en el numerador
Dado que está cambiando el punto decimal en un dígito para hacer 0.5 un número entero, es una buena idea colocar el punto decimal encima de la barra de división exactamente donde se desplaza el punto decimal, es decir, después de los últimos 5 en 655.

Paso 5. Resuelve el problema con una división larga simple
Para dividir 655 entre 5, los pasos son:
- Divida el dígito de las centenas del numerador (6) por el denominador (5). El resultado es 1 con un resto de 1. Escribe el número 1 encima de la barra divisoria y escribe 5 debajo del número 6 que se restará.
- El resto de 1 se resta del dígito de las decenas del numerador (5) para obtener 15. Divida 15 entre 5 para obtener 3. Escriba 3 encima de la barra divisoria, a la derecha de 1.
- Suelta los últimos 5 dígitos. Divide 5 entre 5 para obtener 1. Escribe el número 1 encima de la barra divisoria, a la derecha del número 3. No hay resto porque 5 es divisible entre 5.
- La respuesta de división secuencial larga es 655 5 = 131. Este resultado es el mismo que la respuesta a las preguntas 65.5 0.5.






