- Autor Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-19 22:12.
- Última modificación 2025-01-23 12:15.
El valor posicional, o el concepto de que el valor de un número (0-9) está determinado por su posición en un número en particular, es un concepto fundamental en matemáticas. Dado que este concepto es tan fácil para las personas que ya lo entienden, enseñarlo puede resultar bastante complicado. Sin embargo, una vez que los estudiantes comprendan este concepto, estarán listos y emocionados para usar sus nuevas habilidades y aprender conceptos matemáticos más complejos.
Paso
Parte 1 de 3: Introducción a los conceptos básicos

Paso 1. Tómese el tiempo para enseñar el valor posicional
Si enseña dentro de un alcance curricular predefinido, ya debería tener una idea de cómo encajar el valor posicional en una gama más amplia de aprendizaje. Si da clases particulares o enseña en casa, la estructura de aprendizaje será más flexible. Planee enseñar el valor posicional en algún momento después de que los estudiantes hayan terminado de aprender a contar y realizar operaciones simples de suma y resta, generalmente alrededor del primer o segundo grado. La comprensión del valor posicional proporcionará una base para que estos niños comprendan conceptos matemáticos más complejos.

Paso 2. Presente el concepto de contar grupos de números
La mayoría de los estudiantes de los niños solo aprenden a contar los números uno por uno: uno… dos… tres… cuatro. Esto es suficiente para sumas y restas básicas, pero sigue siendo demasiado simple para proporcionar una base sólida para comprender funciones más complejas. Antes de enseñarles cómo dividir números grandes en sus respectivos valores posicionales, es una buena idea enseñarles a dividir un grupo de números pequeños en números grandes.
- Enséñeles a sus alumnos a contar dos dos, tres tres, cinco cinco y diez diez. Este es un concepto fundamental que los estudiantes deben comprender antes de aprender sobre el valor posicional.
- En particular, intente crear una fuerte "emoción de diez". Las matemáticas modernas utilizan el número diez como base, lo que facilita que los niños aprendan sistemas más complejos si se acostumbran a pensar de esta manera. Enseñe a sus alumnos a agrupar instintivamente números en grupos de diez.

Paso 3. Repase el concepto de valor posicional
Refresque su comprensión. Asegúrese de comprender completamente este concepto antes de intentar enseñárselo a un grupo de jóvenes estudiantes. En pocas palabras, el valor posicional es la idea de que el valor de un número (0-9) depende de su "lugar" o posición en un número.

Paso 4. Explica la diferencia entre números y números
Los números son símbolos de los diez números básicos que componen todos los números: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Estos números se combinan para formar todos los demás números. Un número puede ser un número (por ejemplo, el número 7), pero solo si no está agrupado con otros números. Cuando se agrupan dos o más números, la secuencia de los números forma el número más grande.
Muestre que por sí solo "1" es el número uno y "7" es el número siete. Cuando se agrupan como "17", los dos números forman el número diecisiete. De manera similar, "3" y "5" juntos forman el número treinta y cinco. Muestre algunos otros ejemplos para que los estudiantes puedan volver a casa entendiendo
Parte 2 de 3: Enseñar mediante ejemplos visuales
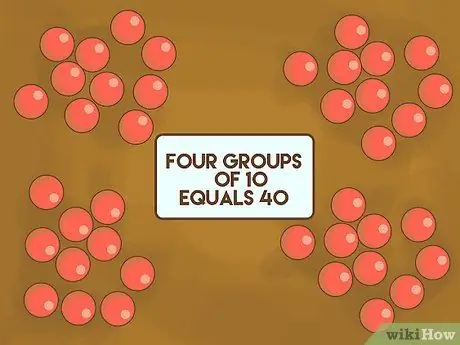
Paso 1. Muestre a los niños que contar de diez a diez es más fácil
Utilice de 30 a 40 objetos que sean pequeños, contables y bastante homogéneos. Por ejemplo: guijarros, canicas o una goma de borrar. Extiéndalo sobre la mesa frente a los estudiantes. Explique que en las matemáticas modernas usamos el número 10 como base. Organice los objetos en varios grupos, luego cuéntelos frente a la clase. Muéstreles que cuatro grupos de 10 guijarros equivalen a 40.

Paso 2. Traduce el ejemplo con guijarros a números escritos
Escriba el bosquejo del concepto en la pizarra. Primero, cree una gráfica T regular. Escriba el número 1 en la esquina superior derecha de la tabla T. Luego, escriba el número 10 en la esquina superior izquierda. Escriba un 0 en la columna de la derecha con la etiqueta "1" y un 4 en la columna de la izquierda con la etiqueta "10". Ahora puede explicar a la clase que cada número hecho con guijarros tiene su propio "lugar".
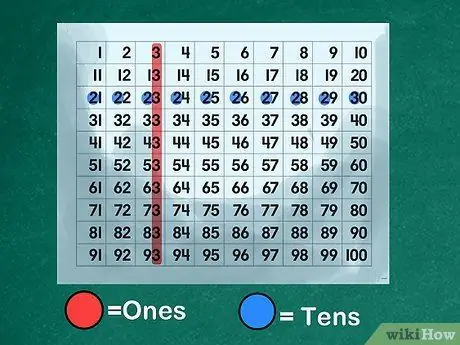
Paso 3. Use un teclado numérico para ilustrar la base del valor posicional
Cree o imprima un "teclado numérico" que muestre todos los números en orden del 1 al 100. Muestre a los estudiantes cómo los números del 0 al 9 interactúan con los números del 10 al 100. Explique que cada número del 10 al 99 se compone de dos dígitos., uno es un número en el lugar de las "unidades" y otro número en el lugar de las "decenas". Muestre que el número "4" representa "cuatro" cuando está en el lugar de "unos", pero sirve como prefijo para el número "40" cuando está en el lugar de "decenas".
- Ilustre el lugar de las "unidades". Indique a la clase que nombre todos los números que tienen el dígito "3" en el lugar de los "unos": 3, 13, 23, 33, 43, 53, 63, 73, 83, 93.
- Explique sobre el lugar de las "decenas". Indique a los estudiantes que designen todos los números que tienen un "2" en lugar de "decenas": 20, 21, 22, 23, 24, 25, 26, 27, 28, 29. Explique que el "3" en "23" es apilados sobre "20" marcados con el número "2". Enseñe a sus hijos a leer el lugar "decenas" como un disparador para el aprendizaje.

Paso 4. Experimente con otras herramientas de enseñanza visual
Puede organizar objetos físicos o dibujarlos en la pizarra. Puede explicar el valor posicional utilizando incrementos de valor monetario, que los estudiantes ya hayan estudiado, para relacionarlos con valores numéricos escalados. Para una actividad divertida e interactiva, intente utilizar a los propios estudiantes como un valor de "grupo".
La memoria humana está dominada por cosas visuales, por lo que el concepto de valor posicional sigue siendo abstracto hasta que pueda hacerlo visual. Mientras tanto, ¡los símbolos numéricos en sí mismos pueden ser abstractos para los niños! Busque formas de enmarcar las actividades de conteo grupal y valor posicional para que sean simples, tangibles e intuitivas
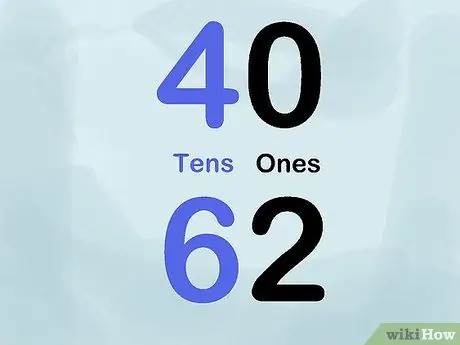
Paso 5. Usa color
Intente usar tizas o marcadores de diferentes colores para demostrar el valor posicional. Por ejemplo, escriba varios números con un marcador negro para el lugar de las "unidades" y un marcador azul para el lugar de las "decenas". Por lo tanto, escribiría 40 con el número "4" en azul y el número "0" en negro. Repita este truco para una gran cantidad de números para mostrar la aplicación del valor posicional en la pizarra.
Parte 3 de 3: Utilice ejemplos interactivos
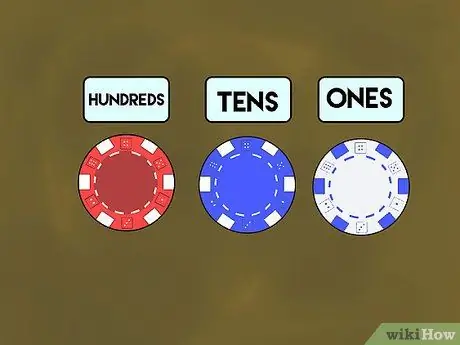
Paso 1. Enseñe con fichas de póquer
Primero, distribuya las fichas de póquer a cada estudiante. Dígales que las fichas blancas representan el lugar de las "unidades", las fichas azules para las "decenas" y las fichas rojas representan las "centenas". A continuación, muestre a sus alumnos cómo hacer números usando valores posicionales en forma de fichas de colores. Nombra un número (digamos 7) y coloca la ficha blanca a la derecha de tu escritorio.
- Nombra otro número, por ejemplo, 30. Pon tres fichas azules que representen 3 (en el lugar de las "decenas") y cero fichas blancas para representar el 0 (en el lugar de las "unidades").
- No tienes que usar fichas de póquer. Puede utilizar cualquier objeto para representar los tres valores básicos de "posición" siempre que cada grupo (color de la ficha, etc.) sea estándar, homogéneo y fácilmente reconocible.

Paso 2. Indique a los estudiantes que intercambien piezas entre ellos
Este método puede ilustrar los valores posicionales bajos que constituyen los valores posicionales más altos. Una vez que los estudiantes hayan demostrado una buena comprensión del valor posicional, enseñe a su clase cómo cambiar las fichas blancas de "unos" por fichas azules de "decenas", luego cambie las fichas de "decenas" por "centenas". Pregunte a los estudiantes: "¿Cuántas fichas azules obtengo al intercambiar 16 fichas blancas? Si cambio tres fichas azules, ¿cuántas fichas blancas obtengo?"

Paso 3. Muestre cómo sumar y restar con fichas de póquer
Este concepto solo se puede enseñar después de que los estudiantes hayan dominado el intercambio de fichas de póquer. Es útil comenzar escribiendo un ejemplo.
- Para el problema básico de suma, pida a los estudiantes que coloquen tres fichas azules (decenas) y seis fichas blancas (unos). Pregunte a los estudiantes sobre los números formados con las fichas. (¡La respuesta es 36!)
- Sigue trabajando en el mismo número. Haga que sus estudiantes agreguen cinco fichas blancas al número 36. Pregúnteles sobre el número actual. (¡La respuesta es 41!) Luego, tome una ficha azul y pregúnteles el número actual. (¡La respuesta es 31!)






