- Autor Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-15 08:13.
- Última modificación 2025-01-23 12:16.
Podría pensar que los números enteros son números ordinarios, como 3, -12, 17, 0, 7000 o -582. Los enteros también se denominan números enteros porque no se dividen en partes como fracciones y decimales. Lea este artículo para aprender todo lo que necesita sobre sumar y restar números enteros, o lea directamente la sección que necesita.
Paso
Método 1 de 5: Sumar y restar números enteros positivos usando una recta numérica

Paso 1. Comprender sobre la recta numérica
Las rectas numéricas convierten las matemáticas básicas en algo tangible y físico que puedes ver. Con solo unos pocos signos y sentido común, podemos usarlo como una calculadora para sumar y restar números.

Paso 2. Dibuja una recta numérica base
Imagina o dibuja una línea recta uniforme. Haz un punto en el medio de tu línea. Escribir 0 o cero junto a este período.
Su libro de matemáticas podría llamar a esto el punto de partida porque es el punto de partida para todos los números

Paso 3. Dibuja dos puntos, uno a la derecha ya la izquierda de tu cero
Escribir - 1 junto al punto de la izquierda y
Paso 1. junto al punto de la derecha. Este es el número entero más cercano a cero.
- No se preocupe por hacer que las distancias entre los puntos sean exactamente iguales; siempre que sepa lo que significa cada punto, se puede usar una recta numérica.
- El lado izquierdo es el comienzo de la oración.

Paso 4. Complete su recta numérica agregando más números
Haga más puntos a la izquierda que -1 y a la derecha que 1. A la izquierda, desde -1, marque sus puntos con - 2, - 3, y - 4. A la derecha, desde el 1, marque su punto con
Paso 2
Paso 3., da
Paso 4.. Puede continuar si tiene espacio en su papel.
El ejemplo de la figura muestra una recta numérica de -6 a 6

Paso 5. Comprender los números enteros positivos y negativos
Enteros positivos, también llamados número natural, es un número entero mayor que cero. 1, 2, 3, 25, 99 y 2007 son números enteros positivos. Los números enteros negativos son números enteros menores que cero (como -2, -4 y -88).
Los enteros son otra forma de llamar a números enteros. Las fracciones como 1/2 (la mitad) son solo una parte del número, por lo que no son números enteros. Igual que decimal, por ejemplo 0,25 (cero coma dos cinco); decimal no es un número entero

Paso 6. Empiece a resolver 1 + 2 colocando su dedo en el punto 1
Resolveremos problemas simples de suma. 1+2 usando la recta numérica que acaba de crear. El primer numero es
Paso 1., así que empieza a señalar el número.
-
¿Es esta pregunta demasiado fácil?
Si alguna vez ha agregado, probablemente sepa la respuesta a 1 + 2. Bien: si conoce el resultado, será más fácil entender cómo funciona la recta numérica. Luego, puede usar la recta numérica para resolver problemas de suma más difíciles o prepararse para matemáticas más difíciles como el álgebra.

Paso 7. Sume 1 + 2 moviendo el dedo 2 puntos hacia la derecha
Desliza tu dedo hacia la derecha, contando el número de puntos (otro número) que pasas. Si ha pasado 2 puntos nuevos, deténgase. El número al que apunta tu dedo es la respuesta,
Paso 3
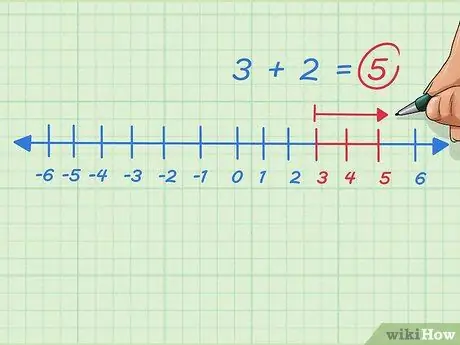
Paso 8. Suma cualquier número entero positivo moviéndote hacia la derecha en la recta numérica
Supongamos que queremos resolver 3 + 2. Comience en 3, muévase hacia la derecha o agregue 2 puntos. Nos detenemos en 5. El problema se escribe 3 + 2 = 5.

Paso 9. Reste números enteros positivos moviéndose hacia la izquierda en la recta numérica
Por ejemplo, queremos resolver 6 -4, comenzamos en 6, nos movemos hacia la izquierda 4 puntos y nos detenemos en 2. Este problema se escribe 6 - 4 = 2.
Método 2 de 5: Sumar y restar números negativos usando una recta numérica

Paso 1. Aprenda sobre las rectas numéricas
Si no sabe cómo crear una recta numérica, regrese a la sección Sumar y restar números positivos usando rectas numéricas para aprender cómo crear una.
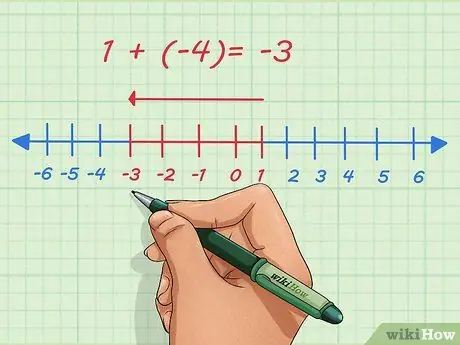
Paso 2. Comprender los números negativos
Los números positivos se indican mediante la dirección a la derecha de la recta numérica. Los números negativos se indican a la izquierda en la recta numérica. Sumar números negativos significa mover el punto hacia la izquierda en la recta numérica.
-
Por ejemplo, agreguemos 1 y -4. Por lo general, esta pregunta se escribe así:
1 + (-4)
. En la recta numérica, comenzamos en 1, nos movemos 4 puntos hacia la izquierda y nos detenemos en -3.
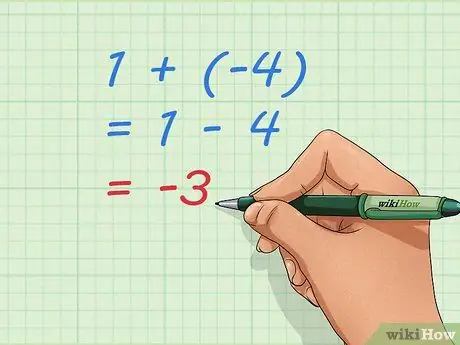
Paso 3. Usa ecuaciones básicas para comprender la suma de números negativos
Observe que -3, nuestra respuesta, es el número que obtendremos si hacemos 1 - 4. Sumar 1 + (-4) y restar 4 de 1 es el mismo problema. Podemos escribirlo como una ecuación, una oración matemática que muestra igualdad: 1 + (-4) = 1 - 4 = -3
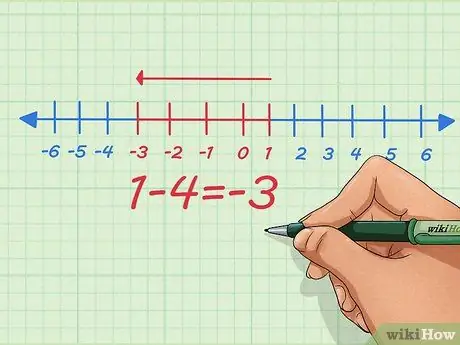
Paso 4. En lugar de sumar números negativos, conviértalo en un problema de resta usando números positivos
Como podemos ver en la ecuación simple anterior, podemos hacer ambas cosas: convertir la suma de números negativos en la resta de números positivos y viceversa. Es posible que le hayan enseñado a convertir los negativos en negativos sin saber por qué, aquí está el por qué.
-
Por ejemplo, -4. Cuando sumamos -4 y 1, restamos 1 por 4. Se puede escribir en matemáticas escribiendo
1 + (-4) = 1 - 4
. Podemos escribir esto en la recta numérica, comenzando en nuestro punto de partida en 1, luego agregando 4 puntos a la izquierda (en otras palabras, agregando -4). Dado que esta es una ecuación, una cosa es igual a otra, por lo que lo contrario también es cierto
1 - 4 = 1 + (-4)
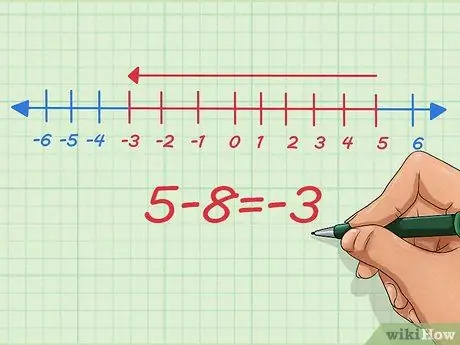
Paso 5. Comprender cómo restar números negativos en una recta numérica
En la recta numérica, restar números negativos es lo mismo que reducir la longitud. Comencemos con 5-8.
En la recta numérica, comenzamos en nuestro punto de partida en 5, restamos 8 y nos detenemos en -3
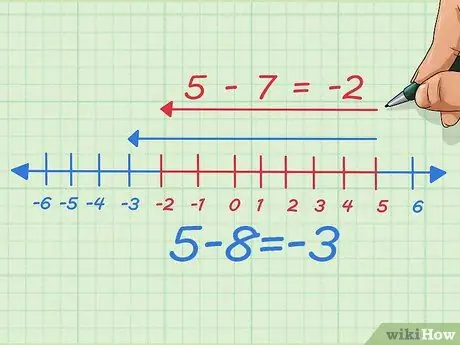
Paso 6. Reste la cantidad que está restando y vea qué sucede
Supongamos que restamos uno, el número que restamos, o en otras palabras, restamos 7 en lugar de 8. Ahora restamos un punto a la izquierda en la recta numérica. Por escrito, comenzamos con 5 - 8 = -3 Ahora, simplemente movemos 7 hacia la izquierda, por lo que se convierte en 5 - 7 = -2
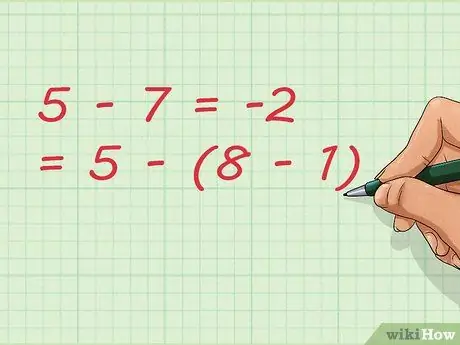
Paso 7. Observe que restar puede resultar en una suma
En nuestro ejemplo, estamos restando el número 1. Al escribir la ecuación, podemos escribirla más corta como: 5 - 7 = -2 = 5 - (8 - 1)

Paso 8. Convierta los signos negativos en positivos al sumar números negativos
Usando el paso de convertir todas las restas en sumas, podemos escribir otras más cortas como: 5 - (8 - 1) = 5 - 7 = 5 - 8 + 1.
-
Ya sabemos que 5-8 = -3, así que saca 5-8 de la ecuación e ingresa -3:
5 - (8 - 1) = 5 - 7 = -3 + 1
-
Ya sabemos que 5 - (8 - 1) es - resta un punto de 5 - 8. Nuestra ecuación puede mostrar que 5 - 8 es igual a -3, y restar un punto da -2. La ecuación se puede escribir así:
-3 - (-1) = -3 + 1
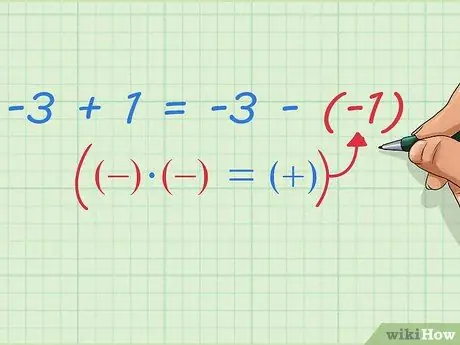
Paso 9. Escribe la resta de números negativos como suma
Observe lo que sucede después de esto; ya hemos demostrado que: -3 + 1 = -3 - (-1) Podemos escribir esto con reglas de escritura matemáticas más simples y generales: primer número más segundo número = primer número menos (segundo número negativo) O, una forma más simple que probablemente hayas escuchado en la clase de matemáticas: Cambie los dos signos negativos en un signo positivo..
Método 3 de 5: Sumar números enteros grandes positivos

Paso 1. Escribe el problema de suma de 2,503 + 7,461 con un número sobre el otro
Escriba los números en la columna grande de modo que 2 sea mayor que 7, 5 sea mayor que 4, y así sucesivamente. De esta manera, aprenderemos a sumar números enteros que son demasiado grandes para imaginar o usar la recta numérica.
Escriba un signo + a la izquierda del número de abajo y la línea debajo de él, como puede aprender para problemas de suma más pequeños
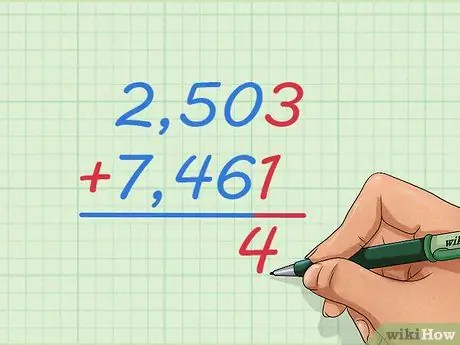
Paso 2. Empiece sumando los dos números del extremo derecho
Puede resultar un poco extraño empezar desde la derecha porque leemos los números desde la izquierda. Tenemos que agregar desde la derecha para obtener la respuesta correcta, que puede ver más adelante.
-
Debajo de los dos números de la derecha,
Paso 3. da
Paso 1., escribe la suma de los dos
Paso 4..

Paso 3. Sume cada número en la columna de la misma manera
Mover a la izquierda, sumar 0+6, 5+4, y 2+7. Escribe la respuesta debajo de cada par de números.
Tu respuesta debería ser: 9.964. Revise su trabajo si comete un error.

Paso 4. Ahora sume 857 + 135
Notarás algo diferente tan pronto como sumes el primer par de números a la derecha. 7+5 es igual a 12, un número de dos dígitos, pero solo puede escribir un dígito debajo de esa columna. Siga leyendo para descubrir qué debe hacer y por qué siempre debe comenzar por la derecha y no por la izquierda.

Paso 5. Sume 7 + 5 y aprenda dónde escribir la respuesta
7 + 5 = 12, pero no puedes poner 1 y 2 debajo de la línea. Pero, anote el último dígito, Paso 2., debajo de la línea y anote el primer dígito
Paso 1., encima de la columna de la izquierda, 5 + 3.
-
Si tiene curiosidad sobre cómo funciona, piense en lo que significa dividir 1 y 2. En realidad, está dividiendo 12 en
Paso 10. da
Paso 2.. Puede escribir 10 encima del número si lo desea, y verá 1 en las columnas 5 y 3, como antes.

Paso 6. Sume 1 + 5 + 3 para obtener el siguiente dígito de la respuesta
Ahora tiene tres dígitos para sumar porque agregó 1 a esta columna. La respuesta es
Paso 9., entonces tu respuesta se convierte en 92.
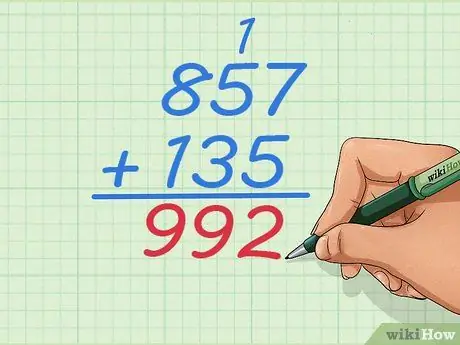
Paso 7. Complete el problema como de costumbre
Siga trabajando los dígitos de la izquierda hasta que haya sumado todos los números, en este caso, solo queda una columna. Tu respuesta final debería ser 992.
- Puede intentar preguntas más complicadas, como 974 + 568. Recuerde, siempre que obtenga un número de dos dígitos, solo escriba el último dígito como respuesta y coloque el otro dígito sobre la columna de la izquierda, que sumará a continuación. Si la respuesta en la última columna (a la izquierda) contiene dos dígitos, escríbala como su respuesta.
- Consulte la sección Consejos para obtener respuestas a las preguntas 974 + 568 una vez que haya intentado resolverlas.
Método 4 de 5: Restar números enteros grandes positivos

Paso 1. Escribe el problema de resta 4.713 - 502 con el primer número sobre el segundo
Escríbalo de modo que 3 esté directamente encima de 2, 1 esté por encima de 0, 7 esté por encima de 5 y 4 esté por encima del espacio en blanco.
Puede escribir 0 debajo de 4 si esto le ayuda a recordar qué número está por encima de qué número. Siempre puede agregar un 0 delante de un número sin cambiarlo. Asegúrese de agregarlo antes del número, no después

Paso 2. Reste cada número de abajo del número directamente arriba
Empiece siempre por la derecha. Resuelve 3-2, 1-0, 7-5 y 4-0, escribe la respuesta a cada pregunta directamente debajo de los dos números restados.
El resultado es, 4.211.

Paso 3. Ahora escriba las preguntas 924 - 518 de la misma manera
Estos números tienen el mismo número de dígitos, por lo que puede escribirlos fácilmente. Este problema le enseñará algo sobre restar números enteros si aún no lo sabe.

Paso 4. Aprenda a resolver el primer problema, que se encuentra en el extremo derecho
4 - 8. Este problema es complicado porque 4 es menor que 8, pero no use números negativos, pero siga estos pasos:
- En la fila superior, cruce 2 y escriba 1. El 2 debe estar a la izquierda del 4.
- Cruce 4 y escriba 14. Haga esto en un espacio estrecho para que quede claro que 14 es más de 8. También puede escribir 1 delante de 4 para hacer 14 si hay suficiente espacio.
- Lo que acaba de hacer es pedir prestado 1 del lugar de las decenas o la segunda columna de la derecha y convertirlo a 10 en el lugar de las unidades o de la columna del extremo derecho. Una vez que el número 10 es igual a diez veces el número 1, entonces es lo mismo.

Paso 5. Ahora resuelve los problemas 14 - 8 y escribe la respuesta debajo de la columna de la derecha
Debería haber escrito 6 en la línea de respuesta más a la derecha.

Paso 6. Complete la siguiente columna a la izquierda, usando el nuevo número que anotó
La resta debe ser 1 - 1, que es igual a 0.
Tu respuesta debería ser ahora 06.

Paso 7. Resuelva el problema completando la última resta, la columna más a la izquierda
9 - 5 = 4, entonces tu respuesta final es 406.

Paso 8. Ahora resolvemos el problema de restar números grandes de números pequeños
Suponga que se le pide que complete 415,990 - 968,772. Escriba el segundo número debajo del primer número y se dará cuenta de que el número de abajo es más grande. Puede saberlo inmediatamente desde el primer dígito de la izquierda: 9 es mayor que 4, por lo que los números que comienzan con 9 son más grandes.
Asegúrese de escribir la columna correctamente antes de comparar. 912 no mayor que 5000 puedes saber si escribes la columna correctamente porque no hay números por debajo de 5. Puedes agregar cero ayuda, por ejemplo, escribe 912 con 0912 para que la columna sea igual a 5000.

Paso 9. Escriba el número más pequeño debajo del número más grande y agregue un signo - delante de la respuesta
Siempre que resta un número de un número más pequeño, el resultado es un número negativo. Es mejor escribir este signo antes de restar para que no se olvide de anotarlo.

Paso 10. Para responder, reste el número pequeño del número grande y recuerde escribir el signo -
Su respuesta será negativa, que se indica con un signo -. No intenta restar un número grande de un número pequeño, luego hace que el resultado sea negativo; tu respuesta será incorrecta.
El nuevo problema a resolver es: 968,772 - 415,990 = -? Consulte la sección Consejos para obtener la respuesta después de intentar resolver este problema
Método 5 de 5: Sumar y restar números enteros negativos
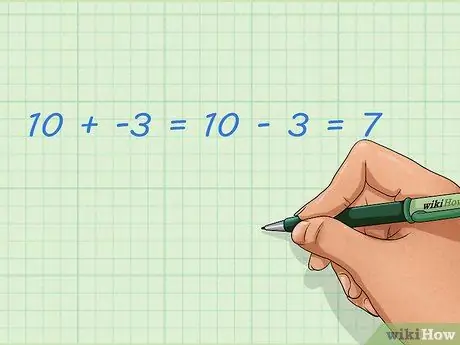
Paso 1. Aprenda a sumar números negativos y positivos
Sumar números enteros negativos es lo mismo que restar números enteros positivos. Esto es más fácil de hacer con la recta numérica descrita en otra sección, pero también puede pensar en ella con palabras. Los números negativos no son números ordinarios; este número es menor que cero y puede representar la cantidad tomada. Si agrega esta toma a un número regular, el resultado se vuelve más pequeño.
- Ejemplo: 10 + -3 = 10 - 3 = 7
- Ejemplo: -12 + 18 = 18 + -12 = 18 - 12 = 6. Recuerda que siempre puedes cambiar el orden de los números en suma, pero no en resta.
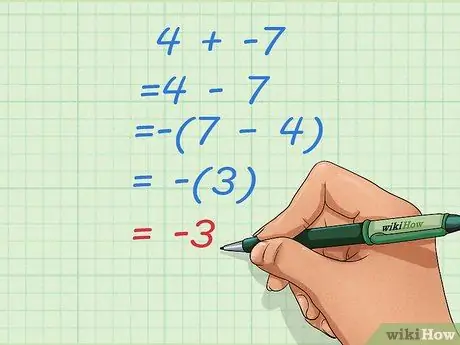
Paso 2. Aprenda lo que tiene que hacer si lo convierte en un problema de resta con un número inicial más pequeño
A veces, cambiar problemas de suma por resta como el anterior puede llevar a respuestas impares como 4 - 7. Cuando esto suceda, invierta el orden de los números y haga que su resultado sea negativo.
- Digamos que su problema inicial es 4 + -7.
- Conviértalo en un problema de resta: 4 - 7
- Invierta el orden y haga que el resultado sea negativo: - (7 - 4) = - (3) = -3.
- Si no está familiarizado con el uso de corchetes en las ecuaciones, piense en esto: 4 - 7 se convierte en 7 - 4 con la adición de un signo negativo. 7 - 4 = 3, pero tenemos que cambiarlo a -3 para que la respuesta a las preguntas 4 - 7 sea correcta.
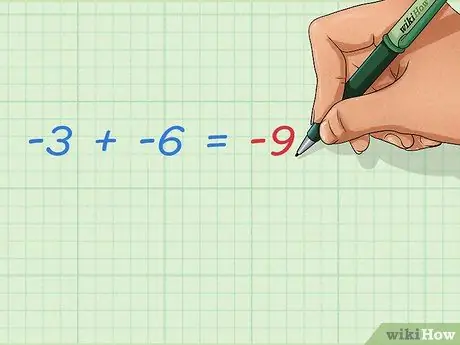
Paso 3. Aprenda a sumar dos números enteros negativos
La suma de dos números negativos siempre hace que el resultado negativo sea más grande. Dado que no se suman números positivos, el resultado estará más lejos de 0. La respuesta es fácil:
- -3 + -6 = -9
- -15 + -5 = -20
- ¿Ves el patrón? Todo lo que tienes que hacer es sumar los números como si fueran números positivos y agregar un signo negativo. -4 + -3 = - (4 + 3) = -7
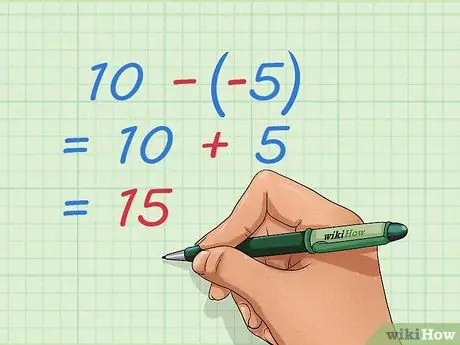
Paso 4. Aprenda a restar números enteros negativos
Al igual que en el problema de la suma, puedes reescribir el problema de modo que solo tengas números positivos. Si resta números negativos, elimina algunas de las cosas que ya se han tomado, lo que es lo mismo que sumar números positivos.
- Piense en los números negativos como dinero robado. Si restas o quitas dinero robado para poder devolverlo, es como darle dinero a alguien, ¿verdad?
- Ejemplo: 10 - -5 = 10 + 5 = 15
- Ejemplo: -1 - -2 = -1 + 2. Ya aprendiste a resolver este problema en el primer paso, ¿recuerdas? Vuelva a leer cómo sumar números negativos y positivos si se le olvidó.
- Aquí está la solución completa del último ejemplo: -1 - -2 = -1 + 2 = 2 + -1 = 2-1 = 1.
Consejos
- Es posible que haya escrito números largos como 2,521,301 usando comas (,) en lugar de (.) Dependiendo de dónde viva. Usa lo que tu profesor te pida para no confundirte con otros sistemas de escritura.
- Dibuja tus rectas numéricas en diferentes escalas para representar diferentes números. No existe una regla de que cada distancia en una recta numérica sea igual a 1. Imagina una recta numérica que es 10 en lugar de 1. Aparte del hecho de que cada punto es 10 ahora, la suma y la resta siguen siendo las mismas. Pruébelo si no lo cree.
- Si prueba las preguntas de desafío especiales en la sección de números largos, aquí está la respuesta: 974 + 568 = 1.542. La respuesta de 415,990 - 968,772 es - 552.782.






