- Autor Jason Gerald gerald@how-what-advice.com.
- Public 2023-12-16 11:06.
- Última modificación 2025-01-23 12:16.
El sistema numérico decimal (base diez) tiene diez valores posibles (0, 1, 2, 3, 4, 5, 6, 7, 8 o 9) para cada posición numérica. En contraste, el sistema numérico binario (base dos) tiene solo dos valores posibles representados por 0 y 1 para cada posición numérica. Dado que el sistema numérico binario es el lenguaje interno de las computadoras electrónicas, los programadores informáticos serios saben cómo convertir del sistema numérico decimal a binario. Siga estos sencillos pasos y también cómo dominar esta conversión.
Paso
Método 1 de 2: División corta por dos con resto

Paso 1. Determine el problema
Para este ejemplo, convierta el número decimal 15610 ser un número binario. Escriba el número decimal como el número que se dividirá en el símbolo de división invertido. Escriba la base del sistema numérico de destino (en este ejemplo, “2” para binario) como el divisor fuera de curva del símbolo de división.
- Este método es mucho más fácil de entender cuando se dibuja en papel y mucho más fácil para los principiantes, porque solo se divide por dos.
- Para evitar confusiones antes y después de la conversión, escriba el número base del sistema numérico que está calculando como un subíndice (minúsculas escritas debajo de letras normales como signo distintivo) para cada número. En este ejemplo, el número decimal tendrá un subíndice de 10 y el número binario tendrá un subíndice de 2.

Paso 2. Haz la división
Escriba la respuesta entera (cociente) debajo del símbolo de división larga y escriba el resto (0 o 1) a la derecha del número dividido.
Debido a que dividimos por dos, cuando el número que se divide es un número par, el resto es 0, y cuando el número que se divide es un número impar, el resto es 1

Paso 3. Continúe dividiendo hasta que llegue a cero
Continúe cuesta abajo, dividiendo cada nuevo cociente por dos y escribiendo el resto a la derecha de cada número dividido. Detente cuando el cociente sea cero.

Paso 4. Anote el nuevo número binario
Comenzando por el número restante más bajo, lea el orden del resto en orden ascendente hasta la parte superior. En este ejemplo, debería obtener el resultado 10011100. Este es el equivalente binario del número decimal 156. O, si se escribe con su subíndice de base numérica: 15610 = 100111002.
Este método se puede modificar para convertir de base decimal a cualquier base numérica. El divisor es 2 porque la base del sistema numérico de destino es la base 2 (binario). Si la base del sistema numérico de destino es otra base, reemplace el número base 2 en este método con el número base apropiado. Por ejemplo, si la base de destino es la base 9, reemplace el número de la base 2 por 9. El resultado final será directamente en la forma del número de la base de destino
Método 2 de 2: derivación de la potencia de dos y la resta

Paso 1. Empiece por crear una tabla
Escriba las potencias de los dos números base en la "base de la tabla 2" de derecha a izquierda. Empiece en 20, escríbalo como "1". Sube el rango en 1 para cada rango. Complete la tabla hasta que obtenga el número más cercano al número del sistema numérico decimal que está calculando. Para este ejemplo, convierta el número decimal 15610 ser un número binario.

Paso 2. Encuentra el número con la mayor potencia del número base 2
De la tabla, elija el número más grande que sea igual o menor que el número a convertir. El número 128 es el número con la potencia más grande del número base 2 y también es menor que 156, así que escribe un número "1" debajo de este cuadro en la tabla, donde el número más grande de la tabla está a la izquierda (ver tabla en la imagen de arriba). Luego reste 128 del número inicial, obtendrá: 156-128 = 28.
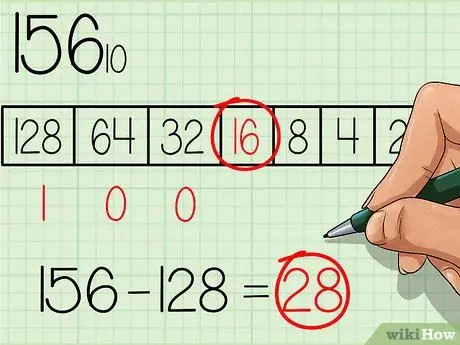
Paso 3. Continúe con la siguiente potencia más pequeña de la tabla
Usando el nuevo número (28), continúe a través de la tabla de izquierda a derecha mientras verifica si los números son iguales o menores que el nuevo número. El número 64 no es menor que 28, así que escriba el número "0" debajo del cuadro de número 64. Continúe hasta que encuentre un número que sea igual o menor que 28.
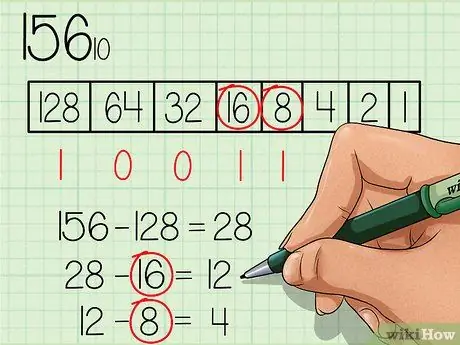
Paso 4. Reste cada número que sea igual o menor que el nuevo número continuamente y marque el número “1” debajo del cuadro para el número apropiado
El número 16 es menor que 28, por lo tanto, escriba el número "1" debajo del cuadro numérico 16 y reste 16 de 28, por lo que obtendrá un nuevo número 12. El número 8 es menor que 12, así que escriba el número "1" debajo el cuadro numérico 8 y reste 8 de 12 para obtener el nuevo número 4.

Paso 5. Continúe hasta llegar al final de la mesa
Recuerde marcar un "1" debajo de cada casilla para los números que son iguales o menores que el nuevo número, y un "0" debajo de cada casilla para los números que aún son mayores que el nuevo número.
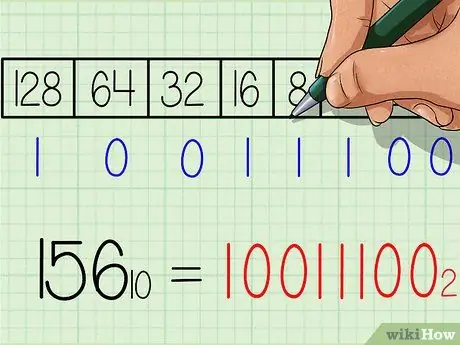
Paso 6. Escriba la respuesta del número binario
El número será exactamente el mismo de izquierda a derecha que la fila de números "1" y "0" en la parte inferior de la tabla. Debería obtener el resultado 10011100. Este es el equivalente binario del número decimal 156. O cuando se escribe con un subíndice: 15610 = 100111002.
Repetir este método puede ayudarlo a recordar los poderes de la base dos, por lo que puede omitir el paso 1
Consejos
- El programa Calculadora integrado en el sistema operativo puede realizar esta conversión por usted, pero como programador, es mejor comenzar con una buena comprensión de cómo funcionan las conversiones. Las opciones de conversión en el programa Calculadora se pueden hacer visibles abriendo el menú "Ver" y seleccionando "Programador" (para Windows 7 y 8).
- La conversión en la dirección opuesta, es decir, del sistema numérico binario al decimal, suele ser más fácil de aprender primero.
- Practique a menudo la conversión de números decimales a binarios para ser más experto.






