Aunque precisión y exactitud a menudo se usan indistintamente, en realidad son palabras muy diferentes en matemáticas y ciencias. Precisión significa que una medición tiene casi el mismo valor cada vez que se realiza. Por ejemplo, si se sube a la báscula 5 veces seguidas, una báscula que tenga buena precisión mostrará la misma masa cada vez. En matemáticas y ciencias, calcular la precisión es muy importante para determinar si sus herramientas y medidas funcionan correctamente para obtener buenos datos. Afortunadamente, calcular la precisión es bastante sencillo.
Paso
Paso 1. Conozca la diferencia entre precisión y exactitud
La precisión mide qué tan bien funcionan sus herramientas, no lo que miden. La precisión comprueba qué tan precisa es su respuesta. Por ejemplo, si su masa es de 9 kg y su balanza muestra 8,7 kg, su balanza no es precisa. Si su balanza muestra 8,7 kg cada vez que pesa su masa, sigue siendo precisa, aunque no exacta.
Piense en las dos palabras en estos términos de tiro con arco: Precisión es si golpeamos el círculo central de la diana de tiro con arco (diana) cada vez que disparamos. Precisión es si damos en el mismo lugar cada vez que disparamos, incluso si ese lugar no es el objetivo que queremos alcanzar.
Paso 2. Registre varias medidas
Para calcular la precisión, necesita datos sobre algo. Por ejemplo, si desea verificar la precisión de su escala, puede pararse sobre ella y registrar el número que se muestra en la escala 15 veces.
Debe registrar varias medidas del mismo objeto en las mismas condiciones para calcular la precisión. No se puede pesar a 10 personas diferentes y comparar los resultados
Paso 3. Encuentre la media o el promedio de sus datos
Para notar el cambio en la precisión, debe comparar sus datos con algo. La media o promedio es el punto central de sus datos y es un buen punto de referencia. Para encontrar la media, sume todas las medidas que tomó y divida el número por la cantidad de medidas que tomó. Si, al pesar su masa, registró las masas: 12 kg, 11 kg, 14 kg, 13 kg y 12 kg, su media sería:
(12 kg + 11 kg + 14 kg + 13 kg + 12 kg) / 5 = 62/5 = 12,4 kg
. En otras palabras, la masa promedio registrada es 12,4 kilogramos.
También puede usar números que ya conoce y no necesita usar la media. Por ejemplo, podría usar una bolsa de papas de 10 kg y comparar sus cifras con este número
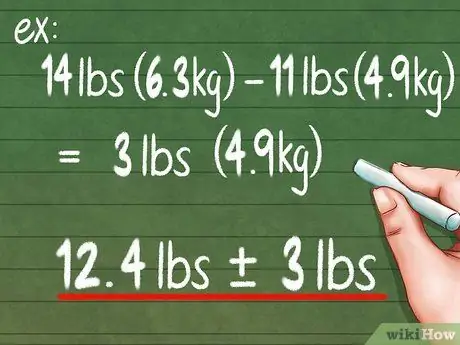
Paso 4. Utilice rangos estándar para cálculos de precisión simples
El rango es la forma más fácil de determinar la precisión. Para calcularlo, simplemente tome su puntaje más alto y reste su puntaje más bajo de ese puntaje más alto. Para el ejemplo anterior, 14 kg - 11 kg = 3 kg. Para que pueda informar que el objeto que está midiendo es 12,4 kg ± 3 kg.
- El valor de ± 3 kg es su medida de precisión. Esto significa que esta escala solo es precisa en el rango de 6 kg o 3 kg más pesada y 3 kg más ligera.
- El símbolo ± se puede leer como "más o menos".
- Este método es el método más utilizado para calcular la precisión. Aunque simple, irónicamente este método no es muy preciso.
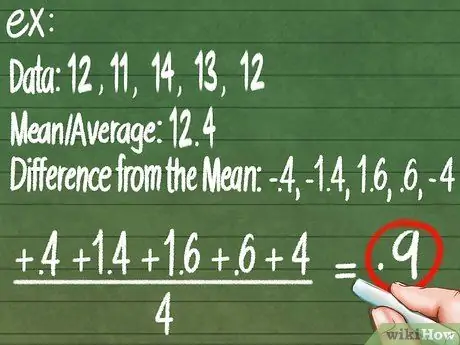
Paso 5. Calcule la desviación absoluta media para obtener una precisión más precisa
Mire de nuevo nuestra media de datos: 12,4 kg. Reste cada medida de la media para encontrar qué tan lejos está cada medida del centro de datos. Haga que todos los números negativos sean positivos. Por ejemplo:
Datos:
12, 11, 14, 13, 12. Media / Media:
12, 4
Diferencia de la media:
-0, 4; -1, 4; 1, 6; 0, 6; -0, 4"
. Ahora, encuentre el promedio de estos números para encontrar qué tan lejos está el promedio de cada medida del centro:
(0, 4 + 1, 4 + 1, 6 + 0, 6 + 0, 4) / 5 = 0, 88. Esto significa que, en general, cualquier medida que tome puede diferir ± 0,88 kg de lo que ve.
Debe ignorar el signo negativo; de lo contrario, los valores se cancelarán entre sí. Recuerde que 11, 4 y 13, 4 son ambos 1 kg de diferencia del promedio de 12, 4, solo que la diferencia es opuesta (positiva o negativa)
Consejos
- Si uno de sus valores de prueba es más alto o más bajo que los demás, no excluya este número de sus cálculos. Incluso si este valor es un error, son datos y deben usarse para cálculos correctos.
- Haga más de 5 intentos para obtener un cálculo más preciso. Cuantos más experimentos haga, más claro será el valor de precisión que obtendrá.
