Con el coeficiente de correlación de rango de Spearman podemos identificar si dos variables tienen una relación de función monótona (es decir, cuando un número aumenta, el otro número también aumentará, o viceversa). Para calcular el coeficiente de correlación de rango de Spearman, debe clasificar y comparar conjuntos de datos para encontrar d2y luego ingrese los datos en la fórmula estándar o simplificada del coeficiente de correlación de rango de Spearman. También puede calcular estos coeficientes usando fórmulas de Excel o el comando R.
Paso
Método 1 de 3: modo manual
Paso 1. Crea una tabla
La tabla se utiliza para incluir toda la información necesaria para calcular el coeficiente de correlación de rango de Spearman. Necesitas una mesa como esta:
- Cree 6 columnas con encabezados, como en el ejemplo.
- Prepare tantas filas en blanco como pares de datos.
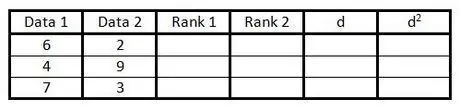
Paso 2. Complete las dos primeras columnas con pares de datos
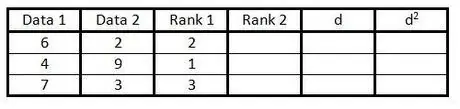
Paso 3. Ingrese la clasificación de la primera columna de grupos de datos en la tercera columna de 1 an (número de datos)
Dé una calificación de 1 para el valor más bajo, una calificación de 2 para el siguiente valor más bajo, y así sucesivamente.
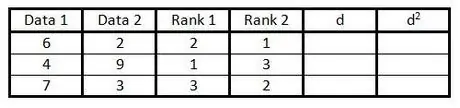
Paso 4. En la cuarta columna, haga lo mismo que en el paso 3, pero para clasificar los datos en la segunda columna
-
Mean_742 Si hay dos (o más) datos que tienen el mismo valor, calcule la calificación promedio de los datos y luego ingréselo en una tabla basada en este valor promedio.
En el ejemplo de la derecha, hay dos valores de 5 en las calificaciones 2 y 3. Como hay dos 5, calcule el promedio de las calificaciones. El promedio de 2 y 3 es 2.5, así que ingrese un valor de calificación de 2.5 para ambos valores 5.
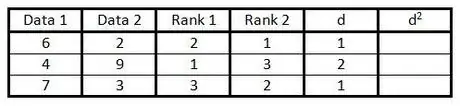
Paso 5. En la columna "d", calcule la diferencia entre los dos números en la columna de clasificación
Es decir, si una columna está clasificada como 1 y la otra columna está clasificada como 3, la diferencia es 2. (El signo no importa, porque el siguiente paso es elevar el valor al cuadrado).
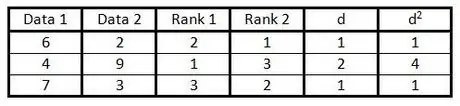
Paso 6. Cuadre cada número en la columna "d" y escriba el resultado en la columna "d2".
Paso 7. Sume todos los datos de la columna d2".
El resultado es d2.
Paso 8. Elija una de las siguientes fórmulas:
-
Si ninguna de las calificaciones es la misma que en el paso anterior, ingrese este valor en la fórmula simplificada del coeficiente de correlación de rango de Spearman
Step8_271 y reemplace "n" con el número de pares de datos para obtener el resultado.
Step9_402 -
Si hay un rango similar en el paso anterior, use la fórmula estándar del coeficiente de correlación de rango de Spearman:
Spearman
Paso 9. Interprete los resultados
El valor puede variar entre -1 y 1.
- Si el valor se acerca a -1, la correlación es negativa.
- Si el valor se acerca a 0, no hay correlación lineal.
- Si el valor se acerca a 1, la correlación es positiva.
Método 2 de 3: usar Excel
Paso 1. Cree una nueva columna para los datos junto con su clasificación
Por ejemplo, si sus datos están en la Columna A2: A11, use la fórmula "= RANK (A2, A $ 2: A $ 11)" y cópielo hasta que cubra todas las columnas y filas.
Paso 2. Cambie la misma clasificación como se describe en los pasos 3 y 4 del método 1
Paso 3. En la nueva celda, calcule la correlación entre las dos columnas de rango con la fórmula "= CORREL (C2: C11, D2: D11)"
En este ejemplo, C y D se refieren a la columna donde se ubica la clasificación. La nueva celda se llenará con la correlación de rango de Spearman.
Método 3 de 3: uso de R
Paso 1. Primero instale el programa R si aún no lo tiene
(Ver
Paso 2. Guarde sus datos en formato CSV, coloque los datos que desea encontrar la correlación en las dos primeras columnas
Podemos hacer esto usando el menú "Guardar como".
Paso 3. Abra R Editor
Si está trabajando desde la terminal, simplemente ejecute R. Si está trabajando desde el escritorio, haga clic en el icono R.
Paso 4. Escriba el siguiente comando:
- d <- read.csv ("NAME_OF_YOUR_CSV.csv") y presione Entrar.
- emitir (rango (d [, 1]), rango (d [, 2]))
Consejos
Los datos deben constar de al menos 5 pares para que se pueda ver la tendencia (el número de datos es 3 pares en el ejemplo solo para simplificar los cálculos)
Advertencia
- El coeficiente de correlación de rango de Spearman solo identifica la fuerza de la correlación cuando los datos aumentan o disminuyen de manera constante. Si hay otra tendencia en los datos, la correlación de rango de Spearman no proporcionará una representación precisa.
- Esta fórmula se basa en el supuesto de que no existen calificaciones iguales. Cuando hay el mismo rango que en el ejemplo, debemos usar esta definición: el coeficiente de correlación del momento de multiplicación por rango.
