El recíproco o recíproco es muy útil en todo tipo de ecuaciones algebraicas. Por ejemplo, cuando divide una fracción por otra, multiplica la primera fracción por el recíproco de la segunda. También necesitas usar la inversa al buscar la ecuación de una línea.
Paso
Método 1 de 3: encontrar el inverso de una fracción o un número entero
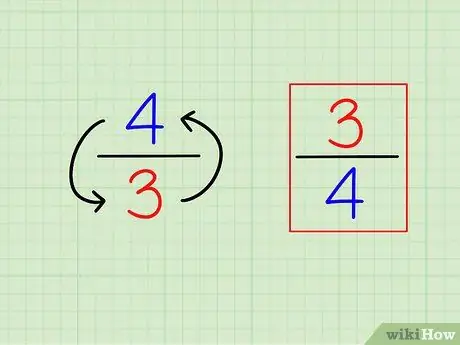
Paso 1. Encuentra el recíproco de la fracción invirtiéndola
La definición de “recíproco” o lo contrario es muy fácil. Para encontrar el recíproco de cualquier número entero, simplemente calcule "1 (ese número)". Para las fracciones, el recíproco es una fracción diferente, es decir, los números están "invertidos" (inversos).
- Por ejemplo, lo contrario de 3/4 es 4/3.
- Cualquier número multiplicado por su recíproco devuelve 1.
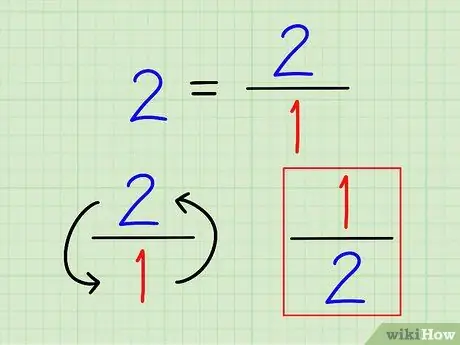
Paso 2. Escribe el recíproco del número entero como fracción
Nuevamente, el recíproco de un número es siempre 1 (ese número). Para números enteros, escríbalos como fracciones. No tiene sentido calcular ese número a un decimal.
Por ejemplo, el recíproco de 2 es 1 2 = 1/2.
Método 2 de 3: Encontrar el inverso de una fracción mixta
Paso 1. Identifica números mixtos
Las fracciones mixtas constan de números enteros y fracciones, como 24/5. Hay dos pasos para encontrar el recíproco de un número mixto como se describe a continuación.
Paso 2. Convierte números mixtos en fracciones impropias
Recuerde que 1 siempre se puede escribir como (número) / (mismo número), y las fracciones con el mismo denominador (número de abajo) se pueden sumar. Aquí hay un ejemplo usando 24/5:
- 24/5
- = 1 + 1 + 4/5
- = 5/5 + 5/5 + 4/5
- = (5+5+4)/5
- = 14/5.
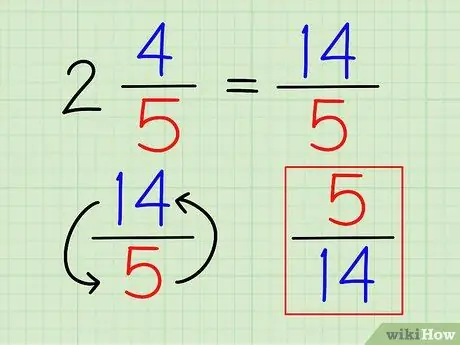
Paso 3. Da la vuelta a la fracción
Una vez que el número se escribe completamente como una fracción, puede encontrar su recíproco como lo haría con cualquier otra fracción, invirtiendo la fracción.
En el ejemplo anterior, el recíproco de 14/5 es 5/14.
Método 3 de 3: Encontrar el opuesto de un decimal
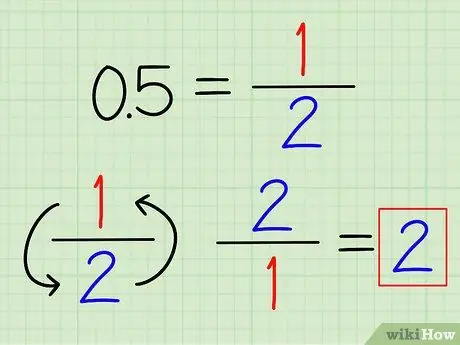
Paso 1. Convierta decimales a fracciones si es posible
Es posible que reconozca algunos números decimales de uso frecuente, que se pueden convertir fácilmente a fracciones. Por ejemplo, 0.5 = 1/2 y 0,25 = 1/4. Una vez que el decimal se ha convertido en una fracción, simplemente voltee la fracción para encontrar su recíproco.
Por ejemplo, el recíproco de 0.5 es 2/1 = 2.
Paso 2. Escribe un problema de división
Si no puede convertirlo en una fracción, calcule el recíproco del número en forma de un problema de división: 1 (decimal). Puede usar una calculadora para resolverlo o continuar con el siguiente paso para resolverlo manualmente.
Por ejemplo, puede encontrar el recíproco de 0,4 calculando 1 0,4
Paso 3. Cambia el problema de división para usar números enteros
El primer paso para dividir decimales es mover el punto decimal hasta que todos los números sean enteros. Siempre que mueva el punto decimal de ambos números en el mismo número de pasos, obtendrá la respuesta correcta.
Por ejemplo, puedes usar 1 0, 4 y reescribirlo como 10 4. En este caso, mueves todos los lugares decimales un paso hacia la derecha, de la misma manera que multiplicas cada número por diez
Paso 4. Resuelve el problema usando una división larga
Utilice el método de división larga para calcular el recíproco. Si cuentas 10 4, obtendrás la respuesta. 2, 5 que es el recíproco de 0, 4.
Consejos
- El recíproco negativo de un número es lo mismo que el recíproco regular, en el sentido de que se multiplica por uno negativo. Por ejemplo, el recíproco negativo de 3/4 es -4/3.
- El recíproco o recíproco a menudo se conoce como el "inverso de la multiplicación".
- El número 1 es opuesto a sí mismo porque 1 1 = 1.
- El número 0 no tiene recíproco porque 0 no está definido.
